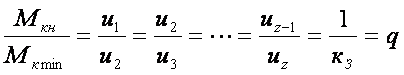Эксплуатационные свойства лесных машин, страница 78

                            .

Таким образом, при равенстве окружных сил на смежных ступенях в момент переключения передаточные числа тракторной трансмиссии формируются по закону геометрической прогрессии со знаменателем q, равным при принятых условиях  обратной величине коэффициента к_з загрузки ДВС по крутящему моменту.

Передаточное число произвольной i-й ступени трансмиссии  .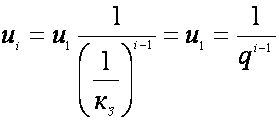

Предположим, что трактор движется на i-й передаче с номинальной загрузкой ДВС (к_з = 1). При этом окружная сила на ведущих колесах будет равна 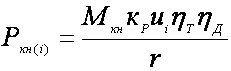 . По мере увеличения внешней нагрузки крутящий момент двигателя растет, а частота вращения коленчатого вала и, соответственно, скорость движения трактора снижается. Чтобы не допустить остановки двигателя от перегрузки, необходимо перейти на пониженную (i - 1) передачу, когда крутящий момент двигателя достигнет максимума, а окружная сила возрастает до 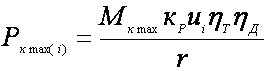. После включения пониженной (i -1)  передачи трогание и разгон трактора идет с окружной силой 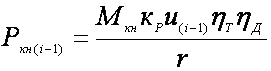 . При равенстве окружных сил до и после переключения  Р_кmax(i) = Р_кн(i-1)  должно быть выполнено и условие      М_кmaxu_iA = М_кнu_(i-1)A , где 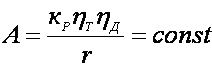 . Тогда 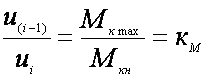 . Из уравнений равенства окружных сил на остальных смежных передачах 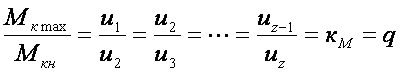   , т.е. и при  таком варианте переключения ступени тракторной трансмиссии распределены по закону геометрической прогрессии. При принятых условиях знаменатель q прогрессии равен коэффициенту к_м приспособляемости двигателя по крутящему моменту. Передаточное число произвольной i-й ступени трансмиссии        .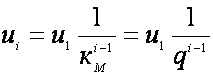

  Из ранее приведенного условия Р*υ = const вытекает, что скорости движения машины, в частности номинальные, также распределены по закону геометрической прогрессии  .