Эксплуатационные свойства лесных машин, страница 170

переднеприводных машин 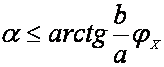       .                      (215)

Возможность преодоления порогового препятствия всей машиной или поездом оценивают по  наименьшему углу.

Выражения (214) и (215) могут быть получены и из уравнений (210) и (211) при j₁=0 для ведомых колес.

Угол a, оценивающий вероятность преодоления порога, может быть выражен через линейные размеры из треугольника АОС (см. рисунок 57)

 ,

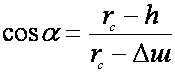откуда величина максимальной высоты h, м,  преодолеваемого порогового препятствия с жесткой кромкой эластичным колесом

h = r_c - (r_c - Dш) cosa  ,                           (216)

где Dш - нормальный (радиальный) прогиб шины, м. При  мягкой (сминаемой) кромке порога величина Dш практически равна разности свободного и статического или расчетного радиусов колеса

                     Dш » (r_c - r) = DВ (1 - l_см).                    (217)

Величины D, В и l_см,  входящие в эту зависимость, указаны в пояснениях к формуле (15). При жесткой кромке порога прогиб эластичной шины значительно возрастает,  и в расчетах его можно принимать равным

Dш = (1,5 - 2,0)×(r_c - r), но не более Dш_max = 0,3В.

Для недеформируемых колес Dш = 0.

Анализ полученных зависимостей  показывает, что высота h преодолеваемого порога возрастает с увеличением свободного радиуса r_c  колеса, толкающей силы Р_х, коэффициентов сцепления  j₁ и j_х, эластичности шины и уменьшается с ростом весовой нагрузки G_к на колесо.

По статистическим данным максимальная высота порогового препятствия для колесных машин не превышает величин, приведенных в таблице 43.

 Таблица 43 - Максимальная высота порога и ширина рва