Эксплуатационные свойства лесных машин, страница 149

Воспользовавшись схемой (см. рисунок 9) сил, действующих на колесный поезд в продольной плоскости при равномерном движении в гору (Р_j = 0) и отсутствии сопротивления воздуха (Р_в = 0), движение возможно при выполнении условия

 Р_j > P_fТ + Р_i + Р_кр .                                     (170)

При задних ведущих колесах

Р_j = SZ_в j_х = Z₂ j_х                                

Нормальная  реакция  Z₂  из  условия  равновесия  системы  относительно точки 0₁

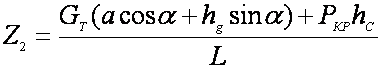                                          (171)

Подставив выражения Р_fт , Р_i и Р_кр в неравенство (170) и уравнение (171) и учитывая, что в пределе сила сцепления при отсутствии буксования (d = 0) равна сумме проекций сил сопротивления движению на опорную поверхность, после преобразований получим уравнение критического угла по буксованию при установившемся движении поезда на подъеме

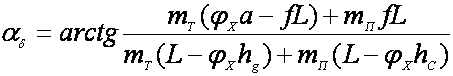       .      (172)

Для одиночного неполноприводного колесного тягача m_п = 0   и

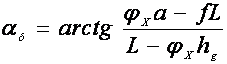                              .                                (173)

Для   гусеничного   и  полноприводного  колесного  тягача    SZ_в =

= G_т j_x сosa. Тогда для поездов с подобными тягачами критический угол по буксованию

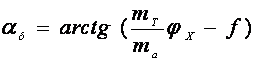                                        ,                           (174)

а для одиночного тягача

a_d  = arctg(j_х - f).(175)

Продольная устойчивость при остановке или стоянке на подъемах и спусках может быть нарушена в результате сползания, когда максимальная тормозная сила недостаточна для удержания машины на наклонной опорной поверхности, то есть Р_тmax < G_аj_хsina. Определение критического угла a_j изложено в оценке удерживающей способности стояночного тормоза.