Коды, построенные таким образом, принято называть укороченными кодами.
Пример 5.11. Из известного кода (5, 3) получить код (4, 2).
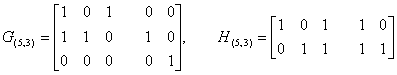
Вычеркиваем из матрицы G(5,3) третью строку и пятый столбец, а из матрицы Н(5,3) пятый столбец. В результате получаем порождающую матрицу и матрицу проверок кода (4, 2):
![]() .
.
Минимальное число линейно независимых столбцов матрицы Н(4,2) по-прежнему равно 2. Следовательно, и dmin этого кода равно 2.
5.3.4. Оценка эффективности групповых кодов
В качестве оценки помехозащищенности помехоустойчивого кода используется вероятность ошибочного приема кодовой комбинации. Для расчета этой вероятности должны быть известны следующие характеристики кода и дискретного канала:
![]() - функция ошибок,
принимающая значения 0 и 1 и указывающая
- функция ошибок,
принимающая значения 0 и 1 и указывающая
выявляется или не выявляется данным кодом конкретный j–тый
образец i-кратной ошибки; j
принимает значения чисел натурального ряда от 1 до ![]() ; i изменяется от 1 до n.
; i изменяется от 1 до n.
![]() - вероятность появления j-го образца i-кратной
ошибки в дискретном канале; определяется либо в результате статистических
испытаний, либо вычисляется аналитически, если известен характер распределения
ошибок и математический закон их описания.
- вероятность появления j-го образца i-кратной
ошибки в дискретном канале; определяется либо в результате статистических
испытаний, либо вычисляется аналитически, если известен характер распределения
ошибок и математический закон их описания.
Вероятность ошибочного приема кодовой комбинации может быть определена как
![]() .
.
Это – точная формула. Однако, в большинстве практических случаев расчеты по данной формуле затруднительны. В тех случаях, когда можно считать вероятности появления различных образцов ошибок кратности i достаточно близкими по значению, т.е.
![]()
приведенная выше формула упрощается и принимает вид
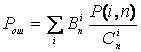 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.