Обработка и передача дискретных сообщений, лекции и материалы, страница 88

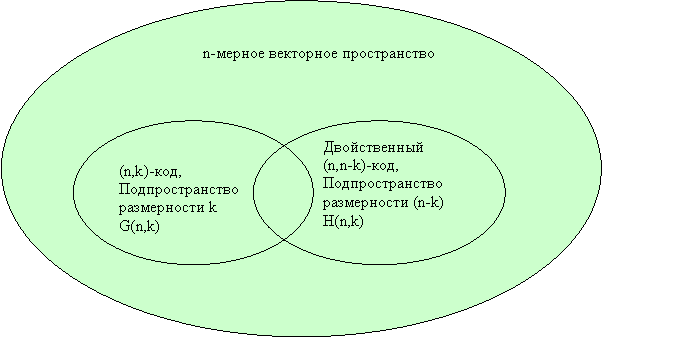
Рис5.5

Векторные подпространства построенные на основе порождающей G(n,k) и проверочной H(n,k)  матриц

         Проверочная матрица позволяет формализовать процесс вычисления проверочных соотношений для любой кодовой комбинации, сведя его к произведению кодовой комбинации на проверочную матрицу по правилам умножения матриц: , то есть некоторая комбинация V принадлежит   (n, k) – коду тогда и только тогда, когда она ортогональна каждой строке матрицы H_{(n, k)}. Соотношение  лежит в основе процедуры декодирования для групповых кодов.

В результате умножения принятой комбинации на матрицу проверок получаем вектор из (n-k) символов, называемый синдромом. В случае, если синдром чисто нулевой, то кодовая комбинация считается принятой безошибочно. При наличии в синдроме ненулевых компонент фиксируется наличие ошибок в кодовой комбинации.

Пример 5.7. Для рассматриваемого выше группового (5, 3) - кода проверочные вектора имеют вид:

1  0  1  1  0               ,

0  1  0  1  1               .

Проверочная матрица:

Двойственный код содержит 4 комбинации:

1  0  1  1  0

0  1  0  1  1

1  1  1  0  1

0  0  0  0  0

Это (5,2) – код с dmin=3

Каноническая форма матрицы H_{(n, k)} имеет следующий вид:

,

где I_n-k – единичная матрица размеров  занимает места, соответствующие избыточным элементам кодовой комбинации;

 - матрица размеров , расположенная на местах, соответствующих информационным элементам; каждая строка этой матрицы указывает, какие информационные элементы кодовой комбинации охвачены проверками на четность.