Обработка и передача дискретных сообщений, лекции и материалы, страница 110

Теорема 5.3. Минимальное кодовое расстояние  итеративного кода равно произведению минимальных кодовых расстояний, кодов, его составляющих.

Действительно, если в случае двух проверок минимальный вес одного кода равен , а другого , то вектор итеративного кода имеет, по крайней мере,  единиц в каждой строке и  элементов в каждом столбце и, следовательно, не менее  единиц.

Аналогичные рассуждения можно продолжить и на случай большего числа проверок.

Порождающая матрица итеративного кода может быть построена следующим образом.

Пусть G_A – порождающая матрица кода, используемого для проверки по строкам, а G_В – порождающая матрица кода, используемого для проверки по столбцам, тогда порождающая матрица итеративного кода (G_AВ) имеет вид:

.

         Запись  означает, что на местах “1” в матрице G_A записывается матрица G_В, а вместо “0” записывается матрица из одних нулей, размеры которой равны размерам G_В. Так, например, если для проверки по строкам и столбцам используется (6, 5) – код с проверкой на четность, то

,

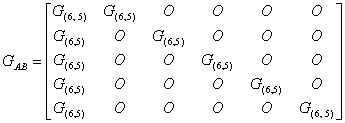где

.

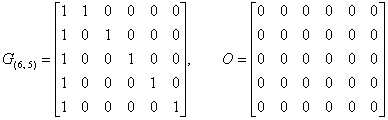5.4.4  Задачи

1. Показать, что корректирующие свойства (6, 5) – кода, в котором избыточный элемент вводится как проверка на нечетность, в точности совпадают с корректирующими свойствами (6, 5) – кода с проверкой на четность.

2. Показать, что коды Хэмминга с d_min=3 соответствуют границе Хэмминга.

3. Показать, что (7, 3) – код, являющийся нулевым пространством кода Хэмминга (7, 4), является эквидистантным, т.е. все кодовые расстояния в этом коде равны.