то есть
многочлен ![]() делится на g(x). Итак,
делится на g(x). Итак, ![]() и есть искомая
кодовая комбинация циклического (n, k) – кода. Отсюда получаем правило построения порождающей
матрицы циклического (n, k)
– кода в канонической форме:
и есть искомая
кодовая комбинация циклического (n, k) – кода. Отсюда получаем правило построения порождающей
матрицы циклического (n, k)
– кода в канонической форме:
![]() ,
,
где Ik – единичная матрица размерности ![]() , соответствующая информационным
элементам кодовых комбинаций,
, соответствующая информационным
элементам кодовых комбинаций, ![]() ;
;
![]() - матрица размерности
- матрица размерности ![]() , j-я
- строка, которой соответствует остатку от деления
, j-я
- строка, которой соответствует остатку от деления ![]() на
g(x).
на
g(x).
Матрица проверок ![]() строится на основании
матрицы
строится на основании
матрицы ![]() по правилу
по правилу
![]() .
.
Пример 6.6. Построить
порождающую матрицу и матрицу проверок в канонической форме для циклического
(7,4) – кода с порождающим многочленом ![]() .
Находим частное и остаток от деления
.
Находим частное и остаток от деления ![]() на g(x) и записываем
результат деления в форме равенства
на g(x) и записываем
результат деления в форме равенства ![]()
|
|


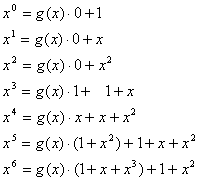
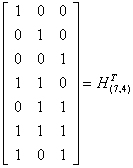
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.