Обработка и передача дискретных сообщений, лекции и материалы, страница 130

Каждый сомножитель двучлена  может быть выбран в качестве порождающего многочлена циклического кода длины n.

Однако не любой сомножитель порождает циклический (n, k) – код с требуемыми корректирующими свойствами. Методика выбора порождающего многочлена для построения циклического кода с заданными корректирующими свойствами будет рассмотрена ниже.

6.3. Построение порождающей и проверочной матриц циклических кодов.

Любой циклический (n, k) – код может быть задан в соответствии с определением 2, порождающим многочленом g(x) или проверочным многочленом .

Знание этих многочленов позволяет построить порождающую матрицу и матрицу проверок. Для циклического (n, k) – кода существует простой способ нахождения k линейно независимых кодовых комбинаций, образующих порождающую матрицу . Этот способ состоит в следующем. Записывается порождающий многочлен g(x). В соответствии с определением 2 комбинация, соответствующая порождающему многочлену, принадлежит циклическому (n, k) – коду. В соответствии с определением 1 циклические сдвиги комбинации, соответствующей g(x), также должны принадлежать этому же коду. Алгебраически сдвиг соответствует умножению кодовой комбинации на х. Так как степень g(x) равна n-k, то подобным образом мы можем получить кодовые комбинации

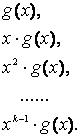
            Легко проверить, что эти кодовые комбинации линейно независимы, хотя бы потому, что степени всех этих многочленов различны, поэтому данный набор многочленов может быть использован в качестве :

.

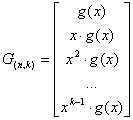Путем элементарных преобразований эта матрица может быть приведена к канонической форме.

Аналогичным образом по проверочному многочлену  можно построить матрицу проверок