Матрица проверок для (n+1, k) – кода Хэмминга с dmin=4 получается из матрицы проверок (n, k) – кода с dmin=3 путем введения дополнительной строки из (n+1)-ой единицы.
Так как размерность матрицы проверок кода с dmin=4
должна быть равна 
, то к каждой строке
матрицы проверок кода с dmin=3, необходимо
добавить один нулевой элемент для того, чтобы не нарушить введенные ранее
проверки. Матрица проверок для (n+1, k) – кода dmin=4
имеет вид:
,
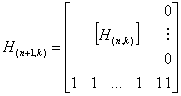где H(n,k) = матрица проверок исходного кода с dmin=3.
Рассмотренная процедура, приведшая к удлинению кодовой комбинации на один разряд при увеличении dmin на 1 единицу, получила название удлинения кода (1- удлинение).Удлинению могут быть подвергнуты и другие коды, например, коды Рида-Соломона.
Пример 5.16. Построить код Хэмминга (8,4) с dmin=4 на основе матрицы проверок кода (7,4).
Известно:
По виду матрицы 
можно сделать
вывод о том, что в коде (7,4) осуществляется 3 независимые проверки на
четность.
Каждая из строк определяет элементы кодовой комбинации, охваченные одной проверкой.
Таким образом, матрице соответствует
следующая система проверочных соотношений:
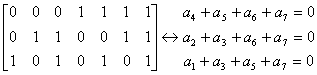
Для того, чтобы получить код (8,4) с dmin=4 вводим еще одну проверку по всем элементам кодовой комбинации, а результат этой проверки записывается в виде дополнительного 8-го элемента:
или
.
Этой проверке соответствует дополнительная (четвертая) строка в матрице Н(8,4), состоящая из восьми единиц. Для того чтобы не нарушить три предыдущие проверки на месте восьмого элемента в трех первых строках матрицы Н(8,4) на месте восьмого элемента, проставляем нули. Итак, матрица проверок кода (8,4) получена в виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.