Зная места проверочных элементов, легко привести матрицу H(n,k) кода Хэмминга к канонической форме.
Для этого необходимо столбцы с номерами 2i, где 
при
упорядоченной записи столбцов переместить на места m
первых столбцов в порядке убывания номеров. В общем виде такая перестановка
столбцов в матрице H(n,k)
приводит к эквивалентному (n, k) – коду. В случае же кодов Хэмминга естественной длины
код получается даже не эквивалентный, а в точности совпадающий с исходным
кодом.
Пример 5.18.
Преобразовать матрицу 
к канонической форме.
Переставим столбцы: 4-ый на место 1-го, 1-ый на место 3-го, а 3-ий на место 4-го:
.
Это и есть каноническая форма матрицы .
Сравнение ее с исходной матрицей показывает, что
местам информационных элементов в канонической форме соответствуют столбцы с
номерами 3, 5, 6, 7, а местам проверочных элементов - столбцы 4, 2, 1.
При этом связи между информационными и избыточными элементами сохранились с учётом их перестановки:
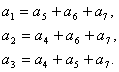
Порождающую матрицу G(n, k) для кода Хэмминга можно получить из матрицы H(n,k), используя теорему 5.3:
Кодирующие и декодирующие устройства для этого класса кодов будут рассмотрены при изучении циклических кодов.
Оценим эффективность кодов Хэмминга.
а) Коды Хэмминга с dmin=3
Такие коды используются либо для исправления ошибки кратности t=1, либо для гарантийного обнаружения ошибок кратности S=2. Соответственно, вероятность ошибки для этих случаев в канале с группированием ошибок равна:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.