Обработка и передача дискретных сообщений, лекции и материалы, страница 52

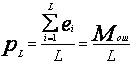
            При достаточно большом  L частость ошибок сходится с вероятностью появления ошибки (вероятность ошибки) p. Значения p для различных типов каналов приведены в таблице 3.1.

            В течение длительного времени, когда отсутствовали статистические данные реальных каналов связи, предполагалось, что ошибки в каналах связи появляются независимо. При таком распределении ошибок значение i-го элемента последовательности ошибок Е не зависит от того, какое значение принимает любой другой j-й элемент данной последовательности.

            Пусть Р{e_i=1}=p, P{(e_i=1)/(e_j=1)} — вероятность приема i-го элемента с ошибкой (e_i=1) при условии, что ошибка произошла на j-м месте (e_j=1), а Р{(e_i=1)/(e_j=0)} — вероятность приема i-го элемента с ошибкой при условии, что j-й элемент принят правильно. Ошибки появляются независимо, если выполняется условие:

            Р{(e_i=1)/(e_j=1)}=Р{(e_i=1)/(e_j=0)}=Р{e_i=1}=p

            В противном случае появление ошибок является зависимым событием.

            При независимых ошибках достаточно знать значение единственного параметра р, чтобы определить распределение любой случайной величины. Для этого достаточно воспользоваться схемой Бернулли. В частности, вероятность появления в n-элементной комбинации ровно i ошибок P(i,n) определяется биномиальным распределением:

                        ( 0 ≤ i ≤ n ).

            Вероятность приема комбинации без ошибки P(0,n)=(1 — p)ⁿ = qⁿ . Следовательно, вероятность появления искаженной комбинации, т.е. комбинации, содержащей хотя бы одну ошибку,

         , при np « 1, P(≥1,n) ≈ np.

            Вероятность появления m и более ошибок в комбинации длины n:

             .