Обработка и передача дискретных сообщений, лекции и материалы, страница 86

1) перестановку любых двух строк;

2) умножение любой строки на скаляр;

3) прибавление произведения одной из строк матрицы на скаляр к другой строке матрицы;

Порождающая матрица (n, k) – кода в канонической форме задает тот же самый код, что и исходная порождающая матрица, т.к. пространства строк этих матриц совпадают в силу выполнения свойства замкнутости.

Пример 5.6. Рассмотрим процедуру приведения матрицы G_{(5, 3)} кода предыдущего примера к канонической форме.

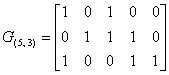
Первая строка матрицы соответствует канонической форме, а вторая и третья должны быть преобразованы. Прибавим ко второй строке первую и результат запишем во второй строке матрицы:

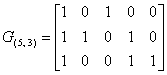
Затем прибавим к третьей строке вторую, а результат запишем в третьей строке

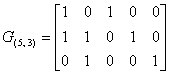
Итак, каноническая форма матрицы кода (5, 3) имеет уже известный вид.

         Следует отметить, что если элементарные операции над строками порождающей матрицы в результате дают в точности тот же самый код, то применение элементарных операций к столбцам матрицы приводит к новому коду, корректирующие свойства которого могут отличаться от свойств исходного кода. Только лишь перестановка столбцов не изменяет весов кодовых комбинаций, а в некоторых случаях и их вида. Поэтому (n, k) – коды, полученные из матрицы  некоторого (n, k) – кода перестановкой столбцов этой матрицы, называют эквивалентными. Таким образом, перестановка столбцов порождающей матрицы (n, k) – кода дает порождающую матрицу для эквивалентного кода (n, k) – кода.

         Заметим, что единичная матрица I_k в канонической форме порождающей матрицы может находиться либо перед матрицей  проверочных элементов, либо после нее в зависимости от того, где в кодовой комбинации располагаются информационные элементы – в начале или конце комбинации. Понятие об эквивалентности кодов позволяет находить каноническую форму порождающей матрицы неразделимого группового кода.