Обработка и передача дискретных сообщений, лекции и материалы, страница 131

.

Пример 6.4. Для циклического (7,4) – кода с порождающим многочленом  (см. пример 6.3.) построить порождающую матрицу.

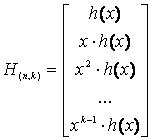
Находим

Следовательно, порождающая матрица для данного кода имеет вид:

            Полученные результаты и рассуждения относительно алгебраической структуры циклических кодов, приведенные в разделе 6.2, позволяют подметить одно важное свойство циклических кодов, определенное их циклической структурой.

Свойство 6.1. Произведение кодовой комбинации циклического кода  на произвольный многочлен дает кодовую комбинацию этого же циклического кода.

Действительно , а любое произведение такого вида равно нулю, т.е. принадлежит кодовому подпространству (раздел 6.2).

Более элементарное доказательство:

.

Полученная сумма есть сумма циклических сдвигов кодовых комбинаций, что по свойству замкнутости группового кода должно дать комбинацию того же циклического кода.

              При описании циклических кодов следует учитывать специфику действий над многочленами, по сравнению с векторами и, в частности, тот факт, что умножение многочленов не совпадает со скалярным умножением векторов, отображающих эти многочлены. Однако в классе вычетов многочленов по модулю  между этими понятиями существует весьма тесная связь. Пусть имеется вектор  и соответствующий ему многочлен , а также вектор  и соответствующий ему многочлен . Будем считать многочлены  и  ортогональными, если выполнено условие .