Вид матрицы ![]() устанавливается
на основе следующего свойства.
устанавливается
на основе следующего свойства.
Свойство 5.4.Если ![]() есть порождающая матрица систематического
(n, k) – кода в
канонической форме, то нулевое пространство этого кода порождается матрицей
есть порождающая матрица систематического
(n, k) – кода в
канонической форме, то нулевое пространство этого кода порождается матрицей ![]() .
.
Доказательство этого свойства основывается на следующих рассуждениях.
Поскольку любая кодовая комбинация при умножении на транспонированную
проверочную матрицу должна давать (n-k) – разрядный нулевой вектор, то этот же результат
должен быть получен при умножении каждой строки порождающей матрицы на
проверочную матрицу, а, следовательно, и умножение матрицы ![]() на матрицу
на матрицу ![]() дает
нулевую матрицу размеров
дает
нулевую матрицу размеров ![]() , т.е. справедливо
равенство
, т.е. справедливо
равенство ![]() .
.
Решение данного матричного уравнения и позволяет установить вид проверочной матрицы:
![]() ,
,
т.е. ![]() или R'=
или R'=![]() .
.
Итак, порождающая матрица (n, k) – кода является сокращенной записью кода. Проверочная матрица указывает соотношение между избыточными и информационными элементами в каждой кодовой комбинации. Между порождающей и проверочной матрицами в канонической форме существует жесткая связь, на основе которой знание одной матрицы позволяет построить другую.
Пример 5.8.
Проиллюстрируем выполнение соотношений ![]() и
и
![]() для кода (5, 3). Порождающая матрица
и транспонированная матрица проверок имеют вид:
для кода (5, 3). Порождающая матрица
и транспонированная матрица проверок имеют вид:
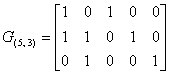
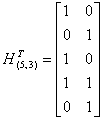
Вычисляем их произведение:
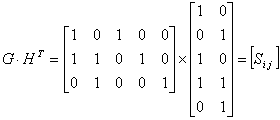
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.