Обработка и передача дискретных сообщений, лекции и материалы, страница 70

в) Минимальное кодовое расстояние для кода, гарантийно обнаруживающего ошибки кратности до S' и исправляющего V кратные ошибки

Рис 5.3

5.1.3.  Классификация помехоустойчивых кодов

Уже отмечалось, что помехоустойчивые коды подразделены на два обширных класса – блоковые и непрерывные коды. Блоковые коды в свою очередь делятся на разделимые и неразделимые коды. Очень часто в разделимых кодах избыточные и информационные элементы связываются между собой системами линейных проверочных соотношений. Такие разделимые коды принято называть систематическими кодами. В силу того, что избыточные элементы в систематических кодах являются результатом проверки на четность определенных информационных элементов, то часто избыточные элементы кодовой комбинации называют проверочными.

На рис. 5.4 приведена схема, иллюстрирующая рассмотренную классификацию помехоустойчивых кодов.

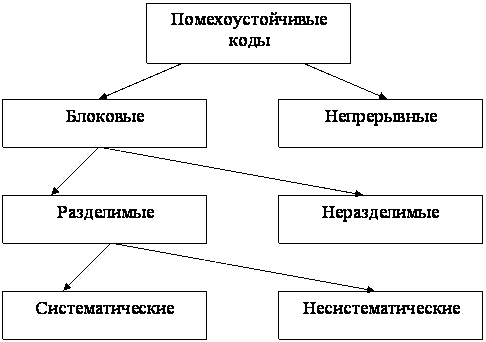Рис.5.4.

5.1.4.Граничные соотношения между характеристиками помехоустойчивых кодов

Одной из важнейших задач построения помехоустойчивого кода с заданными характеристиками является установление соотношения между его способностью обнаруживать или исправлять ошибки и избыточностью, т.е. связь между n – k и d_min. Существует ряд оценок этой связи. Рассмотрим наиболее популярные. Если код предназначен для исправления t – кратных ошибок, то в каждой из 2^k  защитных зон его разрешенных комбинаций должно находиться по  различных комбинаций, а общая их сумма, естественно, не должна превышать числа 2ⁿ, т.е.

, или , т.е. .

 Это соотношение принято называть границей Хэмминга.