Обработка и передача дискретных сообщений, лекции и материалы, страница 137

Пример 6.7. Найти циклические коды длины n=31, исправляющие ошибки кратности t=1, 2, 3.

Определяем l. Так как 31=2⁵-1, то l=5. Находим количество проверочных   элементов для заданных значений t:

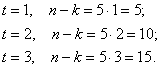
Таким образом, искомые коды (31, 26), (31, 21) и (31, 16).

Следует заметить, что теорема 6.1 определяет лишь существование кодов с известными корректирующими свойствами. Построение же кодов, действительно обладающих этими свойствами, зависит от правильного выбора порождающего многочлена.

              Теорема 6.2. Если среди корней порождающего многочлена циклического       (n, k) – кода имеются корни вида   то минимальное расстояние этого кода равно, по меньшей мере, d.

Циклические коды, удовлетворяющие этим теоремам получили название кодов Боуза-Чоудхури-Хоквингема,или кодов БЧХ по фамилиям их авторов.

Коды БЧХ - обширный класс кодов, предназначенный в первую очередь для исправления многократных ошибок. Коды БЧХ включают в свой состав коды Хэмминга и обобщают их на случай t>1.

Коды БЧХ существуют над полем GF(q), где q≥2. При этом Теорема 6.1., сформулированная для случая q=2, может быть обобщена для q>2. Однако, это обобщение выходит за рамки настоящего учебного пособия. Теорема 6.2. справедлива для q≥2 и будет использована при изучении недвоичных циклических кодов.

Изучение кодов БЧХ является основой для понимания других классов циклических кодов.

6.5. Выбор порождающего многочлена для кода БЧХ

а) Порождающий многочлен для (n, n-1) – кодов.

В примере 6.3 было показано, что один из возможных кодов длины 7 есть (7,6) – код с . Покажем, что этот код образуется на основе проверки на четность всех информационных элементов кодовой комбинации. Для этого определим проверочный многочлен h(x) и построим проверочную матрицу (7,6) – кода. Находим