Обработка и передача дискретных сообщений, лекции и материалы, страница 54

Статистическая вероятность появления искаженной комбинации определяется как отношение числа искаженных комбинаций B_ош(n) к общему числу комбинаций B₀(n), т.е.

                                                .

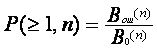Вероятность Р(≥1,n) является неубывающей функцией n. При n=1 Р(≥1,n)=р, а при n→∞ вероятность P(≥1,n) с ростом n зависит от характера распределения ошибок.

На рис. 3.2 показана функция P(≥1,n) в логарифмическом масштабе, т.е. log P(≥1,n)=log p + log n. Это выражение является уравнением прямой, пересекающейся с осью y точке y=p под углом β₁. Так как угловой коэффициент tgβ₁=1, то β₁=π/4.

                        Для гипотетического канала, у которого часть последовательности ошибок e₁= e₂=…= 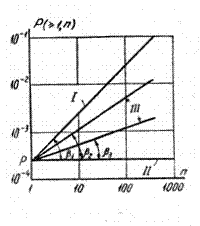e_Мош=1, а остальная часть e_Мош+1= e_Мош+2=…= e_L=0, на интервале  1≤i≤M_ош частость ошибок р_L1 = M_ош / M_ош = 1, а на участке i > M_ош частость ошибок р_L2=0. Так как число искаженных комбинаций длины n B_ош(n)=М_ош / n, а общее число комбинаций B₀ = L / n, то вероятность появления искаженной комбинации:

.

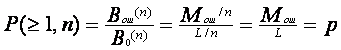Таким образом, для канала, у которого ошибки появляются   плотной   группой   на   одном   из   временных

Рис. 3.2

интервалов,   вероятность   появления   искаженной комбинации не зависит от n и log Р(≥1,n)=log p. Это выражение представляет собой уравнение прямой линии, параллельной оси абсцисс, так как tg β = 0 и β = 0 (прямая II на рис.3.2). Эта прямая пересекается с осью y в точке с ординатой, равной р. Прямые I и II на рис.3.2 являются границами (пределами) зависимости Р(≥1,n) = f(n), т.е. p ≤ Р(≥1,n) ≤ np.

Исследования каналов показали, что для реальных каналов зависимости log Р(≥1,n) = f(log n) достаточно хорошо аппроксимируются прямыми линиями при числе элементов в комбинации от 1 до 500. Прямые, соответствующие этим зависимостям, находятся между указанными выше границами и имеют угол наклона β < β₁ (прямые III на рис.3.2 с углами наклона β₂ и β₃). Такой характер зависимости Р(≥1,n) = f (n) является следствием группового характера появления ошибок в реальных каналах. Для описания зависимости Р(≥1,n) = f (n) достаточно определить значение двух параметров: вероятности ошибки р и углового коэффициента tg β. Обозначим tg β = 1 – α, тогда