Обработка и передача дискретных сообщений, лекции и материалы, страница 47

Приведем интеграл к табулированному значению, получим:

                    .

Пример.

При статистических испытаниях КВ радиоканала получены следующие экспериментальные характеристики распределения дроблений:= 8 мс, ω = 11,5 мс,          γ = 0,45∙ дроблений/мс.

Определим вероятность ошибки при скорости телеграфирования 50 бод для дискретного интегрального метода.

В начале найдем характеристики случайной величины lnτ:

                  ; ;

;

Далее определим нижний предел интегрирования. Так как

                     ,

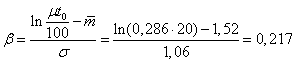то β – σ = 0,217 – 1,06 = -0,743. При β – σ = 0,743 Ф(β – σ) = 0,27.

Таким образом, вероятность ошибки будет равна

3.4.Модели дискретных каналов

3.4.1.Поток ошибок в дискретном канале

На входе и выходе дискретного канала информация представлена в виде последовательности посылок длительностью i (i = 1, 2, 3, …), амплитуда которых может принимать два значения (рис. 3.14 а, б). Каждому значению амплитуды однозначно соответствует «0» или «1», поэтому входную и выходную последовательности дискретного канала можно рассматривать как случайную двоичную последовательность Пусть  является L-элементной двоичной последовательностью на выходе дискретного канала, которая отличается от аналогичной последовательности на входе канала A = () только наличием ошибок. Ошибка это результат неправильного решения регистрирующего устройства о значении принятого единичного элемента в случае, когда величина искажения превышает исправляющую способность.  Результат воздействия различного рода помех может быть представлен так называемой последовательностью ошибок ε (рис. 3.14, в):