Обработка и передача дискретных сообщений, лекции и материалы, страница 148

Действительно, деление обладает свойством суперпозиции, т.е. остаток от деления некоторого многочлена f(x) степени n-1 на порождающий многочлен кода равен сумме остатков от деления степеней xⁱ с ненулевыми коэффициентами из этого многочлена (другими словами степеней xⁱ, соответствующих единицам в принятой кодовой комбинации). Произведение  сводится к суммированию столбцов матрицы Н, соответствующих единицам принятой комбинации. Учитывая, что столбцы матрицы Н – это остатки от деления xⁱ (где ), на порождающий многочлен g(x) находим, что .

Пример 6.13. Определить принадлежность комбинации  циклическому (7,4) – коду с

Вычисляем синдром

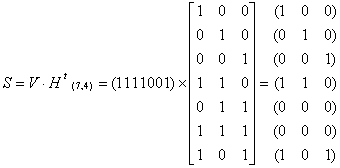
                                                                                     1    0    0

Найдем остаток от деления многочлена  на