Обработка и передача дискретных сообщений, лекции и материалы, страница 76

В результате получаем таблицу следующего вида:

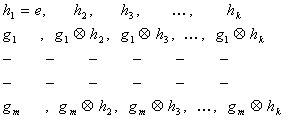
Строки полученной подобным образом таблицы называются смежными классами.

Основные свойства разложения группы на смежные классы по подгруппе формулируются следующим образом:

3. В таблице разложения группы  на смежные классы по подгруппе Н перечисляются все элементы группы , причем каждый элемент появляется в таблице только один раз.

4. Состав смежного класса постоянен и не зависит от выбора образующего элемента.

5. Число элементов в Н является делителем числа элементов в .

6. Два элемента g_i и  g_j    группы G принадлежит одному и тому  смежному классу по подгруппе H тогда и только тогда, когда g_i g_j   принадлежат H.

7. Операция, введенная над элементами группы, может быть введена и над смежными классами. Обозначим{g_i} смежный класс, содержащий элемент группы {g_i} . Тогда {g_i}{g_j}={g_ig_j}, т.е. в результате операции над смежными классами, содержащими элементы g_i и g_j  , получается новый смежный класс, содержащий g_ig_j  . В случае абелевой группы операция над смежными классами приводит к группе, элементами, которой является смежные классы.

Пример 5.2.

Пусть G - группа по операции сложения (т.е. аддитивная группа), состоящая из всех положительных и отрицательных целых чисел и нуля, и пусть H – подгруппа, состоящая из всех чисел, кратных целому числу n. Все числа от нуля до n-1 принадлежат различным смежным классам, т.к. для того, чтобы a и b принадлежали одному смежному классу необходимо, чтобы число (-a)+b принадлежало подгруппе, т.е. было кратно n, что невозможно. Значит, числа от 0 до n-1 могут быть выбраны в качестве образующих смежных классов и других чисел, быть не может. Легко проверить, что группа G -  абелева, поэтому можно ввести операцию сложения смежных классов и смежные классы образуют группу. Положим n=2. Тогда смежные классы имеют вид: