Обработка и передача дискретных сообщений, лекции и материалы, страница 85

         Общее же число наборов k линейно независимых комбинаций из множества 2^k кодовых комбинаций составит число

         Для группового кода (5,3) полное число возможных порождающих матриц оказывается равным

         Столь большое число возможных порождающих матриц для (n, k) - кода затрудняет их использование для задания кода.

         Для однозначности задания кода порождающей матрицей вводят понятие о канонической форме порождающей матрицы.

         Каноническая форма порождающей матрицы имеет следующий вид:

,

где I_k – единичная матрица размерности (k k), то есть такая квадратная матрица, у которой на главной диагонали находятся единицы, а все остальные элементы – нули. I_k содержит информационные элементы кодовых комбинаций, образующих порождающую матрицу.  - матрица размерности , составленная из проверочных элементов базисных кодовых комбинаций.

         Для рассмотренного выше кода (5, 3) каноническая форма порождающей матрицы имеет вид:

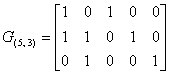
В линейной комбинации строк порождающей матрицы примера 5.5. скаляры при строках в своей совокупности повторяют информационную часть отыскиваемой кодовой комбинации. Из этого вытекает важный вывод: для получения кодовой комбинации (n,k)-кода по ее информационной части необходимо умножить последовательность длины k, являющейся информационной частью кодовой комбинации, на порождающую матрицу этого кода в канонической форме по правилам умножения матриц:

( k- последовательность)×G_(n,k)=[комбинация (n,k)-кода].

Матрица  может быть преобразована к канонической форме при любом исходном наборе базисных кодовых комбинаций посредством элементарных операций над строками матрицы, которые включают: