Обработка и передача дискретных сообщений, лекции и материалы, страница 103

         Этот код является групповым (6, 5) – кодом. Порождающая матрица и матрица проверок этого кода имеют вид:

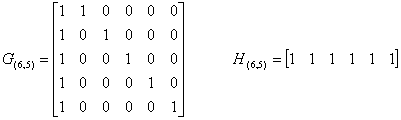
         По виду матрицы Н_(6,5) можно сделать вывод, что данный код имеет d_min=2, т.е. гарантийно обнаруживает все одиночные ошибки.

 Построение кодирующего и декодирующего устройств для (6, 5) – кода, как для циклического кода с порождающим многочленом , будет показано ниже.

         Вероятность необнаружения ошибок (n, n-1) –кода в канале с группированием равна

.

         Вероятность появления ошибок в n – элементной комбинации простого кода равна:

.

         Подсчитаем выигрыш по достоверности, обеспечиваемый (n, n-1) –кодами:

.

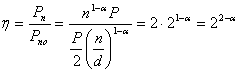         Учитывая пределы изменения показателя группирования , находим, что (n, n-1) – коды обеспечивают повышение достоверности по сравнению с простыми кодами той же длины в  раза.

5.4.2. Коды Хэмминга

         Кодом Хэмминга называется (n, k) – код, который задается матрицей проверок H_(n,k), имеющей  строк и  столбцов, причем столбцами H_(n,k) являются все различные ненулевые двоичные последовательности длины m (m – разрядные двоичные числа от 1 до ).

         Длина кодовой комбинации кода Хэмминга равна .

         Число информационных элементов определяется как .

         Итак, код Хэмминга полностью задается числом m – количеством проверочных элементов в кодовой комбинации.