 .
.
Определим известным способом dmin (8,4) – кода. Из рассмотрения тех столбцов, сумма которых давала нулевой столбец в (7,4) – коде, видно, что с добавлением 4-ой строки они перестали быть линейно зависимыми. Теперь уже число линейно зависимых столбцов должно быть четным и минимум 4, например, 3 первые столбца и последний. Таким образом, для полученного кода Хэмминга (8,4) dmin=4.
До сих пор мы еще не разделили элементы кодовой комбинации на информационные и проверочные. Наиболее рационально, по-видимому, это можно сделать следующим образом. Желательно, чтобы каждое проверочное соотношение однозначно определяло проверочный элемент как результат проверки на четность некоторой совокупности информационных элементов. В таком случае мы получили бы возможность определять значение проверочного элемента наиболее простым образом – решением одного линейного уравнения с одним неизвестным. Для этого при упорядоченной записи столбцов матрицы H(n,k) в качестве проверочных элементов необходимо брать элементы с номерами 2i, где i изменяется от 0 до m-1, так как именно эти столбцы содержат только по одной единице. Последнее свидетельствует о том, что элементы с номерами 2i входят только в одну проверку и, следовательно, они могут быть взяты в качестве проверочных.
Пример 5.17. Определить местоположение проверочных элементов к коде Хэмминга (7,4).
По виду матрицы ![]() , приведенной в
предыдущем примере, в качестве проверочных элементов выбираем элементы, которым
соответствуют столбцы, содержащие только по одной единице, т.е. первый, второй
и четвертый. Следовательно, 4 информационных элемента кода (7,4) должны занимать
места 3, 5, 6 и 7-го разрядов. Приведенная в предыдущем примере система
проверочных соотношений позволяет определить значение каждого из проверочных
элементов по значениям информационных элементов, т.е. по значению элементов
простого кода, который необходимо закодировать кодом Хэмминга
, приведенной в
предыдущем примере, в качестве проверочных элементов выбираем элементы, которым
соответствуют столбцы, содержащие только по одной единице, т.е. первый, второй
и четвертый. Следовательно, 4 информационных элемента кода (7,4) должны занимать
места 3, 5, 6 и 7-го разрядов. Приведенная в предыдущем примере система
проверочных соотношений позволяет определить значение каждого из проверочных
элементов по значениям информационных элементов, т.е. по значению элементов
простого кода, который необходимо закодировать кодом Хэмминга
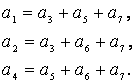
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.