Обработка и передача дискретных сообщений, лекции и материалы, страница 142

Выбор производим по необходимому числу избыточных элементов n-k =15. Так как требуется обеспечить , то по теореме 6.1 принимаем t=2. Ближайшее к требуемому значение избыточных элементов достигается при l=7.

Таким образом, исходным циклическим кодов является (127,113) – код с . Этот код имеет . Следовательно, необходимо добавить еще один избыточный элемент. Для этого умножим g(x) на , т.е. вводим проверку на четность по всем элементам. Получаем (127,112) – код с . Укорочением данного кода на 77 разрядов получаем требуемый код. Итак, в качестве порождающего многочлена для кода (50,35) можно взять . Данный код имеет .

6.6. Эффективность двоичных кодов БЧХ

Для оценки эффективности кодов БЧХ воспользуемся теоремой 5.1, позволяющей установить соотношение между корректирующей способностью кода и его параметрами n и k.

Пусть для циклического (n, k) – кода справедливо  для некоторого l, откуда .

Тогда кратность исправляемых ошибок этим кодов определяется как

.

Минимальное кодовое расстояние может быть найдено из известного соотношения

.

Этих сведений достаточно для краткого анализа эффективности циклического кода в реальном канале с известными параметрами р и α.

Для режима исправления ошибок выигрыш по достоверности по сравнению с простым кодом равен

.

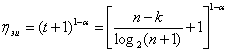Для режима обнаружения ошибок выигрыш составляет

.

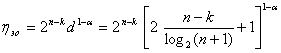Существенным является тот факт, что при исправлении ошибок теоретически возможно обеспечение любой степени повышения достоверности за счет увеличения длины кода n и числа избыточных элементов n - k. Однако практическая реализация таких кодов вызвала бы серьезные затруднения.