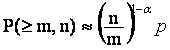
На рис. 3.3 для сравнения пунктирными линиями приведены зависимости Р(≥m,n) = f (m), вычисленные для случая независимых ошибок при том же значении р = 1.37 ·10-2. В этом случае с увеличением m вероятности Р(≥m,n) уменьшаются значительно быстрее, чем те же вероятности, полученные экспериментально. Данный пример показывает, что групповой характер появления ошибок существенно влияет на распределение их внутри комбинаций.
3.4.4 Математические модели дискретных каналов с группированием ошибок
Для аналитического решения задач по определению параметров систем передачи дискретных сообщений находят применение математические модели дискретных каналов, описывающие некоторые закономерности последовательности ошибок. Полнота математической модели определяется в первую очередь решаемыми с ее помощью задачами. Поэтому при описании последовательности ошибок с помощью модели в ряде случаев можно отказываться от некоторых сведений о структуре последовательности при условии, что эти упрощения модели существенно не повлияют на результаты конкретно решаемых задач. Например, в настоящее время преимущественное распространение получили корректирующие коды, в которых результат декодирования зависит лишь от расположения ненулевых элементов в последовательности ошибок и не зависит от их знаков. Поэтому большинство авторов рассматривают модели соответствующие последовательности модулей ошибок
Сводка формул, приведенная выше, базирующаяся на предположении независимого появления ошибок, получила название модели независимых ошибок. Ее математическая основа — схема Я. Бернулли, базирующаяся на знании лишь одного параметра последовательности ошибок — вероятности появления ошибки р.
С точки зрения исследования и проектирования систем передачи дискретных сообщений модель канала связи должна рассматриваться как математическая основа, позволяющая создать приемлемые на практике методы расчета параметров систем. Поэтому естественно предъявить к математическим моделям дискретных каналов следующие основные требования:
1. Соответствие закономерностей распределения ошибок, получаемых при использовании данной модели, действительным закономерностям, наблюдаемым в реальных каналах связи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.