Обработка и передача дискретных сообщений, лекции и материалы, страница 84

            Можно указать несколько троек линейно-независимых комбинаций этого кода. Например:

4.  10100             4.  10100          4.  10100

2.  11010             5.  11101          6.  01110

1.  01001             6.  01110          7.  00111

                                             и так далее.

Каждый из этих наборов комбинаций может служить порождающей матрицей данного    (5, 3) – кода.

Предположим, что в качестве порождающей матрицы данного кода    (5, 3) выбраны кодовые комбинации

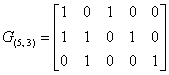
Покажем, что все кодовые комбинации могут быть получены как линейные комбинации базисных векторов, т.е. строк порождающей матрицы:

00000=0(10100)+0(11010)+0(01001),

01001=0(10100)+0(11010)+1(01001),

11010=0(10100)+1(11010)+0(01001),

10011=0(10100)+1(11010)+1(01001),

10100=1(10100)+0(11010)+0(01001),

11101=1(10100)+0(11010)+1(01001),

01110=1(10100)+1(11010)+0(01001),

00111=1(10100)+1(11010)+1(01001).

         Аналогично можно показать, что любой другой набор линейно-независимых комбинаций порождает тот же самый код.

         Преимущество матричного описания кодов очевидно по сравнению с перечислением всех кодовых комбинаций. Действительно, если (n, k) – код содержит 2^k комбинаций, то для его задания требуется всего лишь k кодовых комбинаций.

         Представляет интерес определить число возможных порождающих матриц для групповых кодов с параметрами n и k. Для этого подсчитаем сколькими способами можно набрать k линейно независимых строк порождающей матрицы из 2^k – 1 кодовых комбинаций (чисто нулевая кодовая комбинация, естественно, исключается). В качестве первой строки может быть выбрана любая из 2^k – 1 кодовых комбинаций (т.е. 2^k – 1 способов). Так как среди кодовых комбинаций нет повторяющихся, то в качестве второй строки можно выбрать любую их оставшихся 2^k – 2 комбинаций (2^k – 2 способов). При выборе третьей строки следует исключить из рассмотренных, кроме двух записанных строк, их сумму, т.е. третья строка может быть выбрана 2^k – 2² способами. Рассуждая аналогично, находим, что при выборе i– той строки следует исключить из рассмотрения все линейные комбинации (i - 1) предшествующих строк, т.е. 2^{i – 1} комбинаций.