Учебное пособие по курсу "Теория механизмов и машин", страница 97

Из таблицы следует, что наиболее близкие значения суммарные ординаты удельных скольжений в точках А₂(J_{S. А2}) и А₁(J_{S. А1}) будут иметь при х₁ = 0,6 и х₂ = 0,523. Для таких смещений на ПЭВМ рассчитаны данные для построения диаграмм J₁ и J₂ для 9 характерных точек, которые показаны на рис. 14.26. Распечатка компьютерных данных для построения диаграмм относительных скольжений приведена в табл. 14.5.

Таблица 14.5

Распечатка также содержит:

– длину линии зацепления g = 111,24 мм;

– длину активной линии зацепления g_a = 36,43 мм;

– суммарные ординаты в точках А₂ и А₁ J_{S А2} = 2,05; J_{S А1} = 2,1.

Анализ данных табл. 14.4 показывает, что при постоянном коэффициенте суммы смещений х_S увеличение коэффициента смещения шестерни х₁ снижает коэффициент перекрытия e_a, однако в меньшей степени, чем увеличение суммы смещений.

14.15.2. Коэффициент давления

Коэффициент давления учитывает влияние геометрии зубьев на величину контактных напряжений, возникающих в местах соприкосновения зубьев. Высокие контактные напряжения вызывают выкрашивание рабочей поверхности зубьев. Контактное напряжение определяют по формуле Герца:

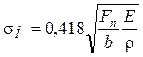                                     ,                          (14.67)

где F_n — нормальное усилие, Н, приложено по нормали к эвольвентной поверхности зуба; b — ширина прямозубого колеса, мм; Е — приведенный модуль упругости, МПа; r — приведенный радиус кривизны, мм.

Помножив и разделив на модуль m подкоренные выражения формулы (14.67), получим:

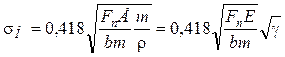                       ,           (14.68)

где g — коэффициент давления,

                          .                        

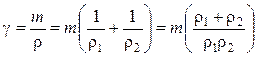С учетом того, что при построении диаграмм r₁ = х, а r₂ = g – x, формула расчета g приобретет вид:

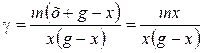                               .                   (14.69)

Диаграмма коэффициента давления g приведена на рис. 14.26, б. Реальные очертания диаграмма имеет в пределах линии зацепления А₂А₁, причем в зонах двухпарного зацепления, определяемых размером основного шага r_b, откладываемого от точек А₂ и А₁ в пределах активной линии зацепления, ординаты делят пополам. Из диаграммы видно, что при однопарном зацеплении наименьшие контактные напряжения возникают вблизи полюса зацепления W и соответственно вблизи полюсной линии на поверхности зуба.

Влияние смещения на контактную прочность зубчатой передачи может быть оценено по расчетной формуле:

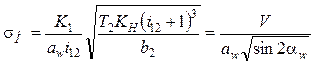                    ,        (14.70)

где K₁ — численный коэффициент; T₂ — вращающий момент на колесе, Н·мм; K_H — коэффициент нагрузки; b₂ — ширина венца колеса, мм; V — параметрический коэффициент, обобщающий все параметры, кроме a_w и .

При увеличении положительного смещения увеличивается угол зацепления. В формуле (14.70) при этом увеличивается знаменатель и снижается рабочее контактное напряжение, что свидетельствует о повышении контактной прочности. В положительном зацеплении межосевое расстояние a_w выше делительного межосевого расстояния a, что создает аналогичный эффект.

NB 14.29. При увеличении суммарного смещения контактная прочность повышается, так как увеличиваются угол зацепления и межосевое расстояние.

14.15.3. Коэффициент формы зуба

Коэффициент формы зуба учитывает изгибную прочность зуба. Лучшей формой является та, которая наиболее приближается к форме балки равного сопротивления изгибу (параболе).