Для определения ускорений кулисы дифференцируют по обобщенной координате φ1 уравнения (5.64) и (5.65). После дифференцирования и вычитания из углов уравнения угла φ3 получают:
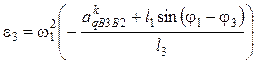 ; (5.70)
; (5.70)
![]() . (5.71)
. (5.71)
В формулах
(5.70) и (5.71) ![]() — аналог кориолисова ускорения:
— аналог кориолисова ускорения:
![]() , где
, где ![]() —
кориолисово ускорение; с учетом формул (5.68) и (5.69):
—
кориолисово ускорение; с учетом формул (5.68) и (5.69):
![]()
![]() (5.72)
(5.72)
![]() —
аналог относительного ускорения:
—
аналог относительного ускорения:
![]() , откуда относительное ускорение с
учетом формулы (5.71):
, откуда относительное ускорение с
учетом формулы (5.71):
![]() (5.73)
(5.73)
Линейные скорости и ускорения точек B3, D, S3 определяют по формулам, аналогичным (5.26) и (5.34):
![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Векторы линейных скоростей направлены перпендикулярно кулисе в сторону вращения. Ускорения точек кулисы имеют две составляющие: an и at. Вектор полного ускорения отклоняется от направления кулисы на угол θа3:
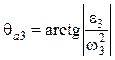 .
.
Значения углов расположения векторов скоростей υ3 и ускорений a3 кулисы 3 определяют по данным табл. 5.6.
Таблица 5.6
|
Знак угловой скорости ω3 |
Углы θυD, θυВ3 и θυS3 векторов скоростей точек D, B3 и S3 |
Знак углового ускорения ε3 |
Углы θаD, θаВ3 и θаS3 векторов ускорений точек D, B3 и S3 |
|
+ |
φ3 + 0,5 π |
+ |
φ3 + π – θа3 |
|
– |
φ3 + 1,5 π |
– |
φ3 + π + θа3 |
Пример 5.3.
Рассчитать по программе ТМ25 кинематические параметры
кривошипно-кулисного механизма для 12 положений кривошипа по исходным данным
примера 4.4: угловая скорость w1 = –15 с-1; длины звеньев: lAB
= 0,1 м; lAC = 0,3 м; lСD = 0,5 м; lCS3 =
= 0,5lCD = 0,25 м; j1
= 0 … 360° с шагом ![]() = 30°.
= 30°.
Решение:
Выполняем расчеты по программе ТМ25 в системе GWBASIC. Распечатка компьютерных данных приведена на рис. 5.9. Данные для сравнения графических (пример 4.4) и аналитических методов приведены в табл. 5.7.
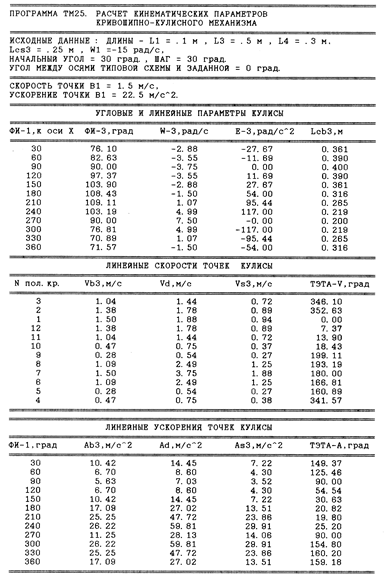
Рис. 5.9
Таблица 5.7
Метод |
w3, с–1 |
ε3, с–2 |
|
|
|
aD, м/с2 |
aB3, м/с2 |
aS3, м/с2 |
Планов |
–2,82 |
28,87 |
1,41 |
1 |
0,7 |
15,13 |
10,75 |
7,5 |
|
Аналитический |
–2,88 |
27,67 |
1,44 |
1,04 |
0,72 |
14,45 |
10,42 |
7,22 |
|
Погрешность, проц. |
–2,1 |
4,3 |
–2,1 |
–3,8 |
–2,8 |
4,7 |
3,2 |
4,2 |
Вывод:
Отклонения находятся в допустимых пределах.
|
Рис. 5.10 |
В различных гидро- и пневмоприводах строительных и путевых машин применяются механизмы с ведущим поршнем на штоке 2, скользящим в качающемся цилиндре (рис. 5.10). Цилиндр 1 по сути является кулисой, т.е. качающейся направляющей, а звено 3 — коромыслом, поэтому механизм иногда называют коромыслово-кулисным. В этом механизме обобщенной координатой принимают переменное расстояние АC = l1. Векторное уравнение замкнутого контура АСD:
![]() .
(5.74)
.
(5.74)
Проекции на координатные оси х и у:
l1 cos φ1 = l3 cos φ3; (5.75)
– l4 + l1 sin φ1 = l3 sin φ3. (5.76)
Из уравнения (5.75) получают:
![]() , или
, или
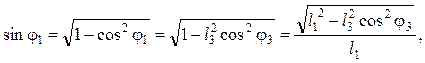 откуда
откуда
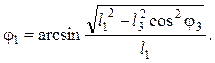 (5.77)
(5.77)
Выражение (5.77) подставляют в уравнение (5.76):
l3 sin φ3
+ l4 = ![]() .
(5.78)
.
(5.78)
После возведения обеих частей равенства (5.78) в квадрат получают
![]() , (5.79)
, (5.79)
или
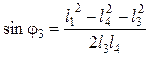 , откуда
, откуда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.