Расчеты по аналитическим зависимостям достаточно сложны и трудоемки для ручного счета. Целесообразно такие расчеты выполнять на ПЭВМ.
Блок-схема алгоритма вышеприведенных расчетов представлена на рис. 5.5. Алгоритм расчета использован в программе ТМ23 «Расчет кинематических параметров кривошипно-коромыслового механизма», составленной автором в системе GWBASIC. Аналитические методы заложены также в программы ТМ24 «Расчет кинематических параметров кривошипно-ползунного механизма», ТМ25 «Расчет кинематических параметров кривошипно-кулисного механизма» и ТММ-1 «Динамический анализ и синтез рычажного механизма ДВС».
|
Рис. 5.5 |
Расчеты на ПЭВМ, излагаемые в текстовом документе, должны содержать:
1) исходные данные: расчетную схему, длины звеньев l, координаты центров масс S и неподвижных точек, угловую скорость ω1, начальный угол поворота кривошипа φ10 и шаг его изменения ∆φ1;
2) алгоритм расчета;
3) распечатку компьютерных данных;
4) анализ с выводом о соответствии аналитического и графического методов с указанием наибольшей ошибки в процентах.
Пример 5.1. Рассчитать по программе ТМ23 кинематические параметры кривошипно-коромыслового механизма по исходным данным примера 4.3: длины звеньев lAB = 0,1 м; lBC = 0,2 м; lCD = 0,3 м; lAD = 0,35 м; lBS2 = = 0,08 м; lDS3 = 0,09 м; угловая скорость кривошипа w1 = 150 с-1, угловая координата кривошипа j1 = 30°.
Решение:
Распечатка компьютерных данных приведена на рис. 5.6. Результаты расчетов кинематических параметров кривошипно-коромыслового механизма графическим методом планов (пример 4.3) и аналитическим методом приведены в табл. 5.4.

Рис. 5.6
Таблица 5.4
|
Метод |
w2, с-1 |
w3, с-1 |
ε2, с-2 |
ε3, с-2 |
υC, м/с |
υS2, м/с |
υS3, м/с |
aC, м/с2 |
aS2, м/с2 |
aS3, м/с2 |
|
Планов |
–71 |
8 |
6000 |
11111,1 |
2,4 |
9,4 |
0,72 |
3333,3 |
2666,7 |
1000 |
|
Аналитический |
–71,08 |
7,64 |
6115,53 |
11189,37 |
2,29 |
9,41 |
0,69 |
3356,86 |
2634,53 |
1007,06 |
|
Погрешность, проц. |
–0,11 |
4,2 |
–1,9 |
–0,7 |
4,8 |
–0,11 |
4,3 |
–0,7 |
1,2 |
–0,7 |
Вывод:
Отклонения рассчитанных параметров укладываются в допустимый предел (5 %).
В центральном кривошипно-ползунном механизме с горизонтальной направляющей (рис. 5.7) заданы: длины звеньев l1 и l2, координаты центра масс шатуна lBS2 и угловая скорость w1. Для упрощения расчетов вводят коэффициенты длины звеньев λ2 = = l2/l1; λS = lBS2/l2. В соответствии с методом замкнутых векторных контуров записывают векторное уравнение в виде:
![]() (5.44)
(5.44)
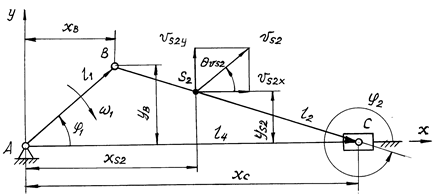
Рис. 5.7
Направляющий угол вектора l2 определяют координатным методом из формулы:
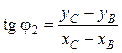 , (5.45)
, (5.45)
где хС, yC и xB, yB — координаты конца С и начала В вектора l2.
yC = 0; yB = l1sin φ1; xC = l1cos φ1 + l2cos φ2; xB = l1cos φ1. (5.46)
Данные из формул (5.46) заносят в формулу (5.45):
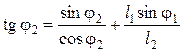 , откуда
, откуда
sin φ2 = –sin φ1/λ2, (5.47)
φ2 = arcsin (–sin φ1/λ2). (5.48)
Кинематические передаточные функции получают дифференцированием выражения (5.48) по обобщенной координате φ1:
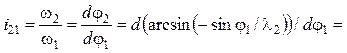
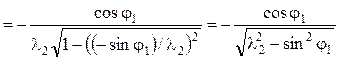 ,
(5.49)
,
(5.49)
откуда с учетом (5.47) угловая скорость шатуна:
![]() . (5.50)
. (5.50)
Угловое ускорение шатуна 2 получают дифференцированием:
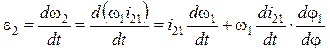 , или
, или
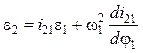 . (5.51)
. (5.51)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.