Учебное пособие по курсу "Теория механизмов и машин", страница 66

Задача имеет множество решений. Так, на рис. 10.9 точки A и D выбраны из условия получения двухкривошипного механизма (самое короткое звено — стойка). Такой механизм показан сплошными линиями в положении стола F₁ и штриховыми — в положении стола F₂. Переход точки B₁ в положение B₂ осуществляется по дуге окружности b, а точки C₁ в C₂ — по дуге c.

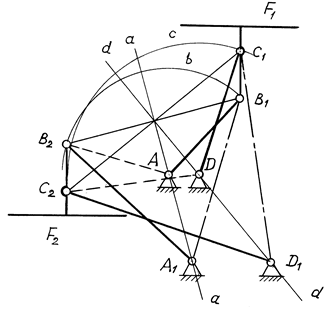
Рис. 10.9

При выборе точек A₁ и D₁ образуется двухкоромысловый механизм (самое короткое звено — шатун). На рис. 10.9 такой механизм показан сплошными линиями в положении F₂ и штрихпунктирными — в положении F₁. Из многих вариантов выбирают наиболее полно удовлетворяющий дополнительным условиям синтеза.

10.6.3. Синтез по заданной траектории точки^*

Известно значительное число механизмов для воспроизведения ряда кривых, размеры которых можно подобрать по справочникам. П.Л. Чебышев с помощью разработанной им теории о функциях, наименее отклоняющихся от нуля, создал множество механизмов, приближенно воспроизводящих заданную траекторию.

На рис. 10.10 изображено лямбдообразное прямило Чебышева с частью траектории точки М, мало отклоняющейся от прямой линии. Такие механизмы применяют в подъемно-транспортном машиностроении (в портальных кранах) и в приборостроении в различных самопишущих приборах. Последнее связано с тем, что механизмы, содержащие только вращательные пары, имеют более легкий ход, чем механизмы с поступательными парами.

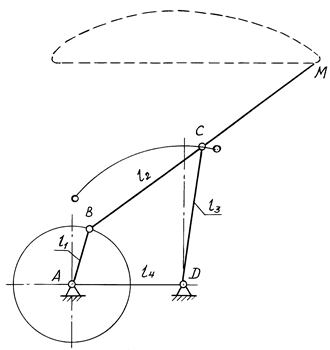
Рис. 10.10

В лямбдообразном прямиле Чебышева приняты длины звеньев:

                                                                    (10.15)

Задача синтеза состоит в определении таких размеров кривошипа  и стойки , которые обеспечивали бы прямолинейность траектории точки М на отдельном участке траектории. П.Л. Чебышевым найдено соотношение лямбдообразного прямила в виде:

                                                                        (10.16)

где  и  — коэффициенты при , определяющие и по соотношениям:

                                                                     (10.17)

Рекомендуется по расчетам Чебышева принимать  [3]. Через параметр  также выражают длину прямолинейного участка L траектории и отклонение  от средней прямой. Не приводя сложных формул, построений и вычислений, запишем ответ:

Так, при L = 435 мм и  = 1 мм рассчитано:  = 196 мм;  = = 99 мм;  = 245 мм. Прямило с такими размерами в масштабе  = = 0,25 мм/мм и траектория точки М изображены на рис. 10.10.

10.7. Синтез кривошипно-ползунного механизма по коэффициенту изменения средней скорости и углу передачи

Исходные данные: ход ползуна H, коэффициент изменения средней скорости К_u и допускаемый угол передачи . Для повышения КПД механизма, уменьшения нагрузок на направляющие ползуна и их износа принимают допускаемый угол давления  = 10 … 30°. Углом передачи μ в данном механизме является угол между направлением шатуна и перпендикуляром к направлению движения ползуна.

Рассчитать длины кривошипа l₁, шатуна l₂ и смещение e.

Откладываем ход ползуна H = C₁C₂ (рис. 10.11). Из середины отрезка C₁C₂ восстанавливаем перпендикуляр и из точки C₁ проводим луч под углом перекрытия θ к перпендикуляру до пересечения с ним в точке О. Радиусом ОС₁ проводим окружность, на которой должны располагаться центры вращения кривошипа.

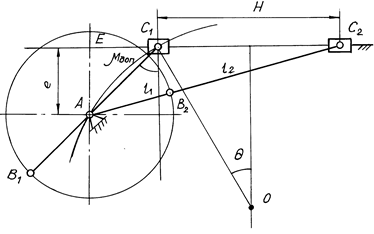
Рис. 10.11

Из точки С₁ под углом μ_доп к перпендикуляру к ходу C₁C₂ проводим луч, определяющий положение центра вращения А. Длины кривошипа l₁ и шатуна l₂ находим аналогично пп. 10.6.1.

Смещение e находят аналитически:

                                                                (10.18)

и проверяют графически:

                                             .                                           

Пример 10.2. Определить длины звеньев l₁, l₂ и смещение e кривошипно-ползунного механизма (см. рис. 10.11) по следующим исходным данным: ход ползуна H = 80 мм; коэффициент изменения средней скорости K = 1,4; допускаемый угол передачи .

Решение:

Угол перекрытия  = 180(1,4 – 1)/(1,4 + 1) = 30.

Масштаб плана положений  = 80/80 = 1 мм/мм.