Учебное пособие по курсу "Теория механизмов и машин", страница 57

NB 9.4. При динамическом уравновешивании необходимо обеспечить равенство нулю главного вектора дисбалансов и главного момента дисбалансов звена.

Динамическую неуравновешенность устраняют двумя корректирующими массами, расположенными в плоскостях коррекции, перпендикулярных оси вращения.

9.4. Статическая балансировка ротора

Для иллюстрации балансировки рассматривается ротор с известными дисбалансами (рис. 9.3). На нем закреплены 5 дисков, из которых диски 1 и 5 — корректирующие, а с дисками 2, 3 и 4 жестко связаны заданные массы m₂, m₃ и m₄.

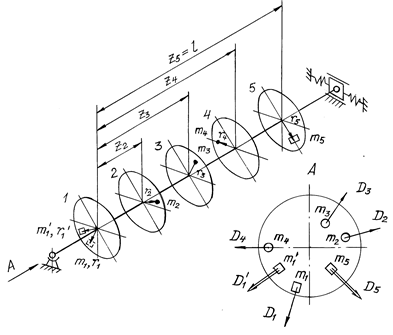
Рис. 9.3

Рассматриваемая схема и методика полностью соответствуют лабораторной работе № 8, выполняемой на типовой лабораторной установке ТММ-35. Пусть центры тяжести заданных масс расположены в трех плоскостях, перпендикулярных оси вращения, на расстояниях r₂, r₃ и r₄ под углами ,  и . Модули дисбалансов масс:

                            D₂ = m₂r₂; D₃ = m₃r₃; D₄ = m₄r₄.                          

При балансировке такого ротора можно было бы каждой неуравновешенной массе противопоставить свою корректирующую массу. Однако такое решение не является рациональным, так как почти всегда происходит частичное уравновешивание дисбалансов. Поэтому применяют другой метод.

Выбирают для выполнения статической балансировки корректирующую плоскость 1, на которой устанавливают корректирующую массу m₁ на расстоянии r₁ под углом . Искомые параметры находят из условия (9.6):

                                                            (9.13)

Векторы ,  и  проводят последовательно в масштабе m_D, мм/(г×мм), под углами соответственно j₂, j₃ и j₄. Вектор  и его направление j₁ находят замыканием векторного многоугольника (рис. 9.4). Для определения угла j₁ конец вектора  переносят в начало координат, а величину j₁ отсчитывают от положительного направления оси x в направлении против часовой стрелки. Модуль D₁ определяют из формулы

                                                                (9.14)

Корректирующую массу m₁ выбирают из набора грузов лабораторной установки (40, 50, 60, 70, 80 г), а радиус-вектор находят из формулы . После установки на диске 1 корректирующей массы ротор должен быть сбалансированным статически. Это означает, что после сообщения ему вращения он останавливается в различных положениях, а не в стабильном, что свидетельствовало бы о дисбалансе.

9.5. Моментная балансировка

Главный момент дисбалансов определяют относительно плоскости приведения, совпадающей с диском 1:

                                                         или

                     ,          (9.15)

где  — расстояния от грузов до плоскости приведения 1.

В число слагаемых не вошел вектор , так как . Для упрощения построений уравнение (9.15) делят на расстояние между дисками 1 и 5 . Если расстояния между соседними дисками одинаковы, что соответствует лабораторной установке ТММ-35, то уравнение (9.15) может быть записано так:

                                                  (9.16)

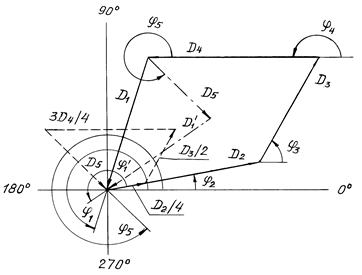
Рис. 9.4

Уравнение (9.16) очень удобно, так как векторный многоугольник моментной балансировки можно построить по векторному многоугольнику статической балансировки, выполненному в масштабе m_D. Для этого из начала координат проводят вектор  в направлении радиуса-вектора , затем векторы  и . Замыканием второго векторного многоугольника (на рис. 9.4 показан штриховой линией) определяют величину и направление искомого вектора . Модуль вектора D₅ = /m_D. Радиус расположения груза

Для моментной балансировки необходимо две корректирующие массы  установить: одну — на диске 5 на расстоянии  под углом , а вторую — на диске 1 под углом  на том же расстоянии.

9.6. Динамическая балансировка

Динамическая, или полная, балансировка предполагает одновременное выполнение условий (9.6) и (9.10). Полная балансировка обеспечивается установкой корректирующих масс в двух плоскостях приведения. В лабораторной установке такими плоскостями являются диски 1 и 5. Из п. 9.4 и 9.5 следует, что на диске 5 необходимо установить массу  для обеспечения моментной балансировки, а на диске 1 по результатам статической и моментной балансировки необходимо установить две массы — m₁ и m₅. Однако конструкция установки этого не позволяет. Обе массы на диске 1 заменяют одной эквивалентной массой. Эту замену выполняют по условию статической балансировки (9.6), так как динамически уравновешенный ротор должен быть и статически уравновешенным: