Учебное пособие по курсу "Теория механизмов и машин", страница 36

2. Разложение векторов. Заданы один вектор, известный по величине и направлению, и два направления p–p и q–q. Требуется определить составляющие вектора. Для этого из начала и конца вектора проводят заданные направления до их взаимного пересечения (рис. 6.8). Уравнение разложения:

                                         .                                (6.6)

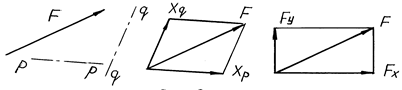
Рис. 6.8

Наиболее просто уравнение (6.6) решается при направлениях, соответствующих координатным осям:

                                          .                                       

3. Векторное уравнение с одним неизвестным.

                                       .                               (6.7)

Так как правая часть уравнения (6.7) равна нулю, искомый вектор Х определяют замыканием векторного многоугольника (рис. 6.9), т.е. проведением вектора из конца последнего вектора в начало первого.

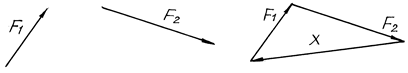
Рис. 6.9

4. Векторное уравнение с двумя неизвестными. Оно может быть решено, если искомые векторы известны по направлению. Например, если они направлены перпендикулярно известным векторам:

                                   .                         (6.8)

Для решения задачи проводят из конца второго вектора  направление , перпендикулярное ему, а из начала первого вектора — перпендикулярное ему направление вектора  до пересечения с  (рис. 6.10).

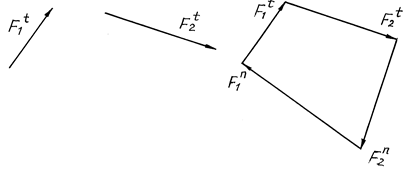
Рис. 6.10

5. Система двух векторных уравнений с двумя неизвестными.

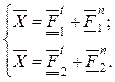                                                                         (6.9)

Из одной точки проводят векторы  и . Из их концов проводят перпендикулярно им направления  и  до их пересечения друг с другом (рис. 6.11) Искомую величину Х определяют по любому уравнению системы (6.9). Определяют также искомые векторы  и .

6.7. Силовой расчет диады 2-го вида графо-аналитическим методом

В кривошипно-ползунном механизме (см. рис. 4.1, а) силовой расчет начинают с диады 2–3, на звено 3 которой действует движущая сила , направленная против скорости . В общем случае силовой расчет начинают с наиболее удаленной диады.

Исходные данные силового расчета: вес звеньев ,  и ; силы инерции звеньев и , направленные противоположно ускорениям соответственно  и ; момент сил инерции , направленный противоположно угловому ускорению ε₂.

Рассчитать: реакции в кинематических парах , , , ; уравнивающий момент ; мгновенную мощность и механический коэффициент полезного действия (КПД).

1. Составление расчетной схемы. Диаду 2–3 вычерчивают в масштабе  в заданном положении (рис. 6.12). В точках В, С и S₂ звеньев прикладывают заданные силы и искомые реакции в кинематических парах. Реакцию в поступательной паре  направляют перпендикулярно направляющей x–x и прикладывают в точке С.

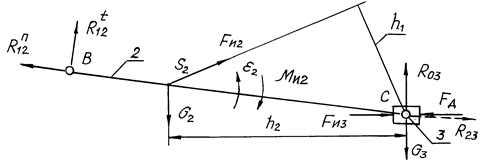
Рис. 6.12

Реакция  во вращательной паре известна лишь по точке приложения В. Для удобства расчетов ее раскладывают на два направления: вдоль звена — нормальная составляющая, перпендикулярно звену — тангенциальная:

                                        .                             (6.10)

                                               || ВС ^ВС                                        

В других случаях (см. п. 6.11) ее раскладывают по координатным осям. План сил позволит определить величины только двух векторов, не известных по величине, но известных по направлению. В данном примере — три неизвестные величины. Величина  может быть получена из аналитического моментного уравнения равновесия.

2. Аналитическое уравнение для звена 2:

                 –,      (6.11)

где , h₁ и h₂ — плечи сил, мм, взятые из плана положений.

Из уравнения (6.11) находят реакцию . Если ее знак окажется отрицательным, то ее направление противоположно изображенному на рис. 6.12. Далее задача имеет векторные решения.

3. Векторное уравнение для диады 2–3.

NB 6.3. Правила составления векторных уравнений:

1. Вначале записывают векторы, известные по величине и направлению; векторы, известные только по направлению, ставят в конец уравнения.

2. Последовательно записывают векторы сил, действующих на звенья: вначале на одно звено, затем на другое.