Точки s2 и s3 находим из свойства подобия планов.
bs2 = 0,4bc = 0,4×46 = 18,4 мм; ps3 = 0,3pc = 0,3×100 = 30 мм.
Соединяем найденные точки с полюсом p. Длины отрезков, изображающих ускорения центров масс:
ps2 = 80 мм; ps3 = 30 мм.
Абсолютные ускорения точек:
aC = pc/ma = 100/0,03 = 3333,3 м/с2;
aS2 = 80/0,03 = 2666,7 м/с2; aS3 = 30/0,03 = 1000 м/с2.
Относительные тангенциальные составляющие:
atCB = n1c/ma = 36/0,03 = 1200 м/с2;
atCD = πc/ma = 100/0,03 = 3333,3 м/с2.
Модули угловых ускорений:
e2 = atCB/lBC = 1200/0,2 = 6000 с-2;
e3 = atCD/lBC = 3333,3/0,3 = 11111,1 с-2.
Угловые ускорения шатуна и коромысла — положительные. Это следует из схем скоростей и ускорений звеньев (рис. 4.3, г, д).
Пример 4.4. Выполнить структурный и кинематический анализ рычажного механизма поперечно-строгального станка (рис. 4.4, а) по следующим исходным данным: угловая скорость кривошипа w1 = –15 с-1; длины звеньев: lAB = 0,1 м; lAC = 0,3 м; lСD = 0,5 м; lDE = = 0,15 м; координаты: y = lCD; lCS3 = 0,5lCD = 0,25 м; lDS4 = 0,5lDE. Угловая координата кривошипа j1 = 150°.
Решение:
1. Строим план положений в масштабе ml = AB/lAB = 20/0,1 = = 200 мм/мм. Длины отрезков на плане положений:
AC = lAC /ml = 0,3×200 = 60 мм; CD = 0,5×200 = 100 мм;
DE = 0,15×200 = 30 мм; CS3 = 0,5×100 = 50 мм;
DS4 = 0,5×0,15×200 = 15 мм.
Откладываем отрезок AB = 20 мм в положении 10 (j1 = 150°). Точку C размещаем на расстоянии AC = 60 мм от точки A, а направляющую x–x — на расстоянии 140 мм от точки C. Проводим направление оси кулисы от точки C через точку B, откладывая CD = 100 мм. Из построения находим CB = 71 мм. Точку E находим методом засечек, проведя дугу окружности радиусом DE = 30 мм до пересечения с направляющей. На звеньях 3 и 4 отмечаем положения центров масс S3 и S4, откладывая отрезки CS3 и DS4.
2. Структурный анализ. Механизм имеет 5 подвижных звеньев: звено 1 — кривошип, 2 — камень кулисы, 3 — кулиса, 4 — шатун, 5 — ползун. Звенья соединяются между собой семью низшими кинематическими парами: пятью вращательными и двумя поступательными. Число степеней свободы по формуле Чебышева W = 3×5 – 2×7 = 1. Отсоединяем вначале диаду 2-го вида 4–5 (рис. 4.4, б), затем диаду 3-го вида 2–3 (рис. 4.4, г). Остается начальный механизм I класса (рис. 4.4, в). Кинематический анализ начинаем с диады 2–3, ближайшей к начальному звену, кинематика которого задана.
3. Для построения плана скоростей составляем систему векторных уравнений. Точка B кинематической схемы принадлежит трем звеньям. Точки B1 и B2 движутся как одно целое. Точка B3 принадлежит кулисе 3 и меняет положение на звене в зависимости от угла поворота кривошипа. Кинематика точки B3 и будет искомой:
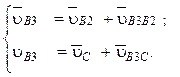(4.30)
Линейная
скорость 
B1 = B2 = w1lAB =
15×0,1 = 1,5 м/с. Масштаб плана
скоростей m
=
pb1/B1 =
75/1,5 = 50 мм/(м×с-1).
Из полюса p
проводим вектор pb1 = 75 мм перпендикулярно AB в сторону вращения (рис. 4.4, д). Из его конца проводим направление B3B2 параллельно звену CD.
Из полюса p (так как C = = 0) проводим
направление B3C
перпендикулярно CD до пересечения с направлением B3B2.
В искомую точку b3 направляем стрелки искомых векторов.
Полученные длины отрезков:
pb3 = 50 мм; b3b2 = 56 мм.
Положения точек d и s3 находим из пропорций:
pd = pb3×CD/B3C = 50×100/71 = 70,4 мм,
ps3 = 0,5×70,4 = 35 мм.
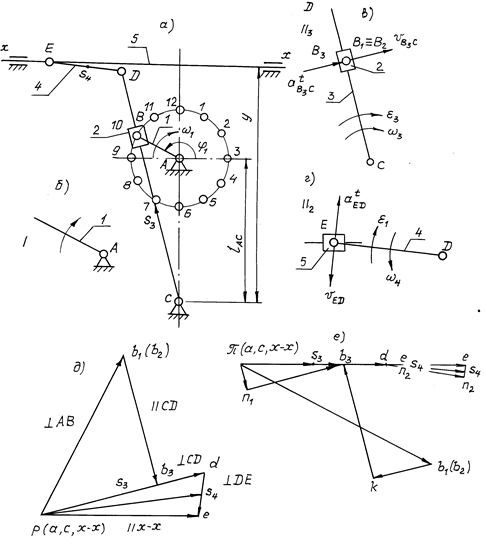
Рис. 4.4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.