Для вращающейся одномассовой динамической модели уравнение (7.1) записывают в виде:
,
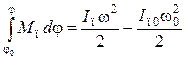(7.8)
где
— значения обобщенной координаты за
конечный промежуток времени; 
— угловая скорость
звена приведения; 
— значение угловой
скорости при 
; 
и 
— моменты инерции в начале и в конце
промежутка времени.
Для того, чтобы уравнения движения (7.1) и (7.6) были тождественными, необходимо и достаточно выполнение двух условий:
;
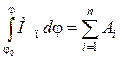(7.9)
.
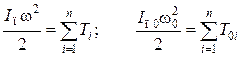(7.10)
Из уравнения
(7.9) находят приведенный момент сил 
, а из (7.10) — приведенный
момент инерции Iп. Более удобным для расчетов является выражение с равенством мощностей,
получаемое дифференцированием выражения (7.9):
.
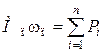(7.11)
Из формулы (7.11) следует:
NB 7.4. Приведенный момент сил Mп(либо приведенная сила Fп) определяется из равенства мощности звена приведения сумме мощностей сил, действующих на звенья механизма.
В общем случае приведенный момент сил равен:
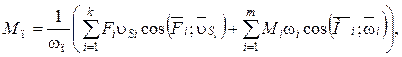(7.12)
где k — число сил, действующих на механизм; m — число моментов, действующих на рычажные звенья механизма.
NB 7.5. Приведенный момент равен
уравновешивающему моменту 
по модулю и
противоположен по направлению.
Из уравнений (7.10) следует:
NB 7.6. Приведенный момент инерции (приведенная масса 
) определяется из
равенства кинетической энергии звена приведения сумме кинетических энергий
звеньев механизма:
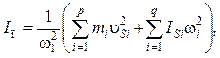(7.13)
где p — число звеньев механизма; q — число вращающихся звеньев.
Пример 7.1. Рассчитать по данным примеров 4.1, 5.2 и 6.1 приведенный к звену 1 момент сил в кривошипно-ползунном механизме (рис. 4.1, а и 6.12).
Исходные данные: угловая скорость кривошипа ω1 = 215 с-1, угловая координата φ1 = 30º, длины звеньев: lAB = 0,08 м, lBС = 0,3 м, координата центра масс шатуна lBS2 = 0,09 м; массы звеньев: m2 = 3,1 кг; m3 = 2,2 кг; момент инерции шатуна IS2 = 0,028 кг∙м2; давление в цилиндре р = 2,9 МПа, диаметр цилиндра dц = 100 мм.
Из решения
примера 5.2 кинематические параметры заданного механизма: угловая скорость
шатуна ω2 = –50,1 с-1; угловое ускорение шатуна ε2 = 5881 с-2; скорость и
ускорение ползуна υС =
= –10,6 м/с; аС = –3713 м/с2; скорость центра масс
шатуна 
S2 =
= 13,91 м/с, θυS2 =
131,4º; ускорение центра масс шатуна аS2 =
= 3597 м/с2, θаS2 = 201,1º.
Решение:
1. Определяем исходные силовые параметры.
Вес звеньев и угол их расположения:
G2 = m2g = 3,1∙9,81 = 30,4 Н; G3 = 2,2∙9,81 = 21,6 Н; θG = 270º.
Силы инерции звеньев:
FИ2 = m2aS2 = 3,1∙3597 = 11151 Н; FИ3 = 2,2∙3713 = 8169 Н.
Силы инерции направлены противоположно ускорениям, т.е.
θFИ = θa ± 1800: θFИ2 = 201,1º – 180º = 21,1º;
θFИ3 = 180º – 180º = 0º.
Момент сил инерции шатуна
МИ2 = –IS2ε2 = –0,028∙5881 = –165 Н∙м.
Движущая сила
FД = –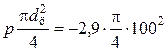
= –22777 Н.
2. Приведенный момент сил — формула (7.12):
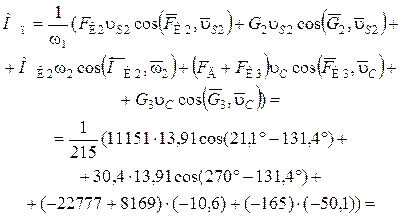
506,9 Н∙м.
Примечания.
1. Векторы, расположенные по оси x, и угловые векторы ставят со своими знаками, косинусы при этом не учитывают.
2. Мп = 506,9 Н∙м = –Му = –527 Н∙м (см. пример 6.1) с ошибкой 3,8%.
Пример
7.2. Рассчитать по данным примера 7.1 приведенный к валу 1 момент инерции Iп.
Исходные данные: угловые скорости: ω1 = –215 с-1, ω2 = –50,1 с-1;
линейные скорости: S2 = 13,91 м/с; С
= –10,6 м/с; массы звеньев: m2 = 3,1 кг; m3 = 2,2 кг; момент инерции кривошипа IS1 =
0,1 кг∙м2, момент инерции шатуна IS2 =
= 0,028 кг∙м2.
Решение:
Приведенный момент инерции — формула (7.13):
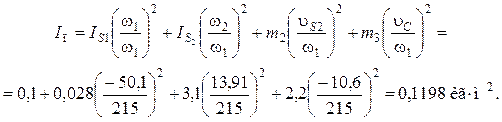
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.