Учебное пособие по курсу "Теория механизмов и машин", страница 45

Кроме уравнений (7.6) и (7.7) в некоторых случаях удобно применить уравнение движения механизма, представленное в форме дифференциального уравнения второго порядка. Его можно получить из уравнения (7.1) в дифференциальной форме: . При вращающемся с угловой скоростью w звене приведения

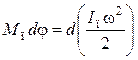                                                                           или

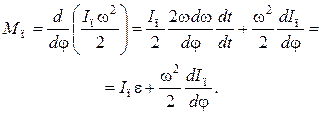                              (7.14)

При , например, в зубчатом механизме с круглыми колесами:

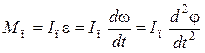                               .                     (7.15)

Получается известное выражение второго закона Ньютона для вращательного движения. При поступательном движении получают аналогичные зависимости:

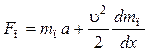                                                                (7.16)

или при

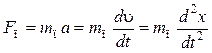                              .                   (7.17)

7.6. Механический коэффициент полезного действия

В механизме кроме сил полезного сопротивления, для преодоления которых он предназначен, действуют силы вредного сопротивления. К последним относятся, прежде всего, силы трения в кинематических парах, силы сопротивления масла при работе зубчатых колес в масляной ванне, силы сопротивления, вызванные жесткостью лент в механизмах с гибкими звеньями, и т.д. Чем меньше потери, тем более совершенным считается механизм. Для оценки этих потерь вводится понятие коэффициента полезного действия механизма(механического КПД).

В установившемся режиме при периодическом движении механизма все звенья имеют одинаковую скорость в начале и конце цикла. Поэтому в уравнении (7.4) работа сил инерции  равна нулю. Принимается также равной нулю работа сил тяжести , так как вес звеньев значительно меньше других нагрузок; тогда уравнение (7.4) приобретает вид:

                                         .                                      

NB 7.7. Механическим коэффициентом полезного действия называется отношение работы сил полезного сопротивления к работе движущих сил за время установившегося движения:

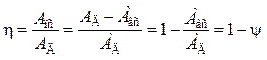                      < 1,            (7.18)

где  — коэффициент потерь.

В уравнение (7.18) вместо работ А_д и А_пс можно подставить мощности:

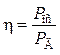                                              .                                   (7.19)

В любом механизме потерь не избежать, поэтому КПД всегда меньше единицы. Но чем выше КПД, тем совершеннее механизм. В соединенных последовательно нескольких механизмах (рис. 7.4) КПД отдельных механизмов:

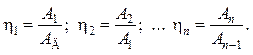                                            (7.20)

По выражению (7.18) общий КПД равен:

                                            .                                          

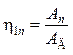Рис. 7.4

После перемножения левых и правых частей уравнений (7.20) получают:

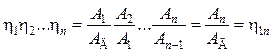                                                 или

                                        .                             (7.21)

NB 7.8. Общий механический КПД последовательно соединенных механизмов равен произведению КПД отдельных механизмов, составляющих одну систему.

Величины КПД различных механизмов определяют экспериментально и указывают в справочниках. Так, например, для зубчатых механизмов  [20] с учетом потерь в подшипниках. Для некоторых механизмов КПД рассчитывают по формулам. В частности, для винтовой пары и червячной передачи:

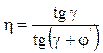                                         ,                               (7.22)

где γ — угол подъема резьбы;  — приведенный угол трения.

Пример 7.3. Рассчитать КПД четырехзаходной червячной передачи (z₁ = 4), если коэффициент трения f = 0,08. Делительный диаметр червяка d₁ = 40 мм, шаг p = 12,57 мм, угол профиля 2a = 40°.

Решение:

Угол подъема резьбы

                  .                

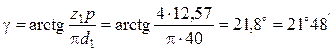Приведенный угол трения

                 .               

Величина КПД

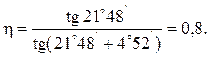
Пример 7.4. В механическом приводе, состоящем из трех ступеней, задано: КПД ременной передачи η_р = 0,95; КПД зубчатой передачи η_з = 0,96; КПД цепной передачи η_ц = 0,93. Рассчитать общий КПД привода.

Решение:

Общий КПД

                          η = η_рη_зη_ц = 0,95×0,96×0,93 = 0,85.