Учебное пособие по курсу "Теория механизмов и машин", страница 6

NB 3.1. Обобщенная координата механизма — одна или несколько угловых или линейных координат звеньев механизма.

Число обобщенных координат равно числу степеней свободы механизма, так как оно показывает, сколько независимых параметров может быть произвольно задано.

Существуют общие закономерности в структуре (строении) различных механизмов, связывающие число степеней свободы механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул кинематической цепи.

Вывод таких формул несложен. Общее число независимых движений n звеньев пространственного механизма равно 6n. Соединение звеньев в кинематические пары накладывает различное число связей (S = 1…5), которое необходимо исключить из 6n степеней свободы. Если число одноподвижных кинематических пар p₁, то общее число связей 5p₁, так как каждая пара имеет 5 связей. Для двухподвижных пар общее число связей 4p₂ и т.д., для пятиподвижных пар общее число связей 1p₅. Таким образом, число степеней свободы

W = 6n – 5p₁ – 4p₂ – 3p₃ – 2p₄ – p₅                            (3.1)

или

                                    W = 6n – 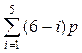_i.                                                         

Формула (3.1) называется структурной формулой кинематической цепи общего вида. Впервые она была дана в 1887 г. П.И. Сомовым и развита в 1923 г. А.П. Малышевым и носит название формулы Малышева. Следует обратить внимание на то, что в формуле Малышева сумма коэффициентов и индексов равна 6.

Пример 3.1. Рассчитать число степеней свободы механизма манипулятора (рис. 3.1).

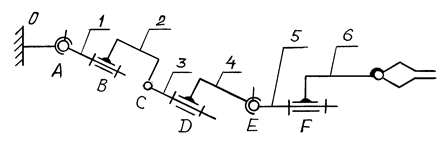
Рис. 3.1

Решение:

Вычерчиваем кинематическую схему механизма. Заданная кинематическая цепь — пространственная незамкнутая. Обозначим характерные точки механизма буквами, номера звеньев — цифрами (стойка обозначается цифрой 0). Составляем таблицу пар и звеньев (табл. 3.1).

Таблица 3.1

В механизме манипулятора число подвижных звеньев n = 6, число одноподвижных кинематических пар (вращательных) p₁ = 4, число двухподвижных пар (сферических с пальцем) p₂ = 2; число степеней свободы W = 6×6 – 5×4 – 4×2 = 8. Это означает, что для работы механизма необходимо иметь 8 источников движения.

Примечания.

1.  Термин «манипулятор» происходит от латинского слова manus — рука. Рука человека, представляющая собой пространственную биомеханическую цепь, содержит 19 звеньев и кинематические пары различного вида — суставы. Расчет по формуле Малышева дает W = 27. Механизмов с таким числом степеней свободы в настоящее время не существует.

2.  Кинематические схемы выполняют по ГОСТ 2.703-68 с использованием элементов кинематики по ГОСТ 2.770-68 (прил. А).

3.  Кинематические схемы выполняют без учета масштаба, но с соблюдением примерных соотношений между элементами механизма.

3.2. Формула Чебышева

Для плоского механизма формула (3.1) преобразуется в следующую:

W = 3n –2p₁ – p_2.                                                    (3.2)

Эта формула была впервые выведена в 1869 г. П.Л. Чебышевым и носит название формулы Чебышева. Она может быть получена из формулы Малышева вычитанием из коэффициентов при n и p числа 3, т.е. разности числа степеней свободы тела в пространстве и на плоскости.

Справедливость формулы Чебышева нетрудно проверить. На плоскости n звеньев имеют 3n степеней свободы. Одноподвижные пары (вращательная и поступательная) имеют на плоскости по 2 условия связи, двухподвижные пары — по одной связи. Общее число связей 2p₁ и p₂ следует вычесть из числа 3n.