Учебное пособие по курсу "Теория механизмов и машин", страница 112

При неравенстве масштабов отрезок , изображающий вектор υ_qB, получают умножением ординаты  диаграммы  = = (φ₁) на отношение масштабов:

                                       .                           (16.13)

К диаграмме υ_qB = υ_qB (S_В) проводят лучи под углами (для фазы удаления) и  (для фазы сближения) к направлению движения толкателя. Точка пересечения этих касательных определяет положение центра вращения кулачка (заштрихованный участок). Центр вращения кулачка необходимо принимать в вершине лучевого треугольника  либо в непосредственной близости от него в заштрихованной области. Соединив точку  с точкой О, получают графическое изображение минимального радиуса кулачка  и смещения . Истинные значения основных параметров:

                                                             (16.14)

Полученные размеры округляют до стандартных по ГОСТ 6636-69. В центральном механизме е = 0 и начальный радиус > > , что приводит к увеличению размеров кулачка. Очевидно, что ужесточение требований по углам давления (их уменьшению) приводит к более низкому расположению точки вершины разрешенной зоны и соответственно к увеличению габаритов кулачка.

На рис. 16.9, г также приведен приблизительный контур кулачка (штриховой линией) с размерами, соответствующими диаграмме  = ().

16.7.3. Аналитический метод

Закон движения толкателя задается в виде функции а_qВ = = а_qB(φ). Например, для косинусоидального закона изменения аналога ускорения линейное ускорение

                                       а_qВ = cos (πφ/φ_у),                            (16.15)

где φ/φ_у = 0, 1, 2, …, n; n — число участков, на которое делят угол удаления; для расчетов на ПЭВМ n = 12.

Закон изменения аналога скорости:

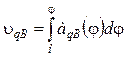                                       .                           (16.16)

Закон перемещения толкателя:

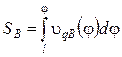                                       .                            (16.17)

Таким образом, для каждого положения толкателя можно рассчитать значения S_B (φ) и _qB (φ), необходимые для определения основных размеров кулачка. Для определения искомых параметров используют теорему о сложении скоростей:

                                          .                              (16.18)

С вращающимся кулачком связывается подвижная система координат n–t, где n–n — нормаль в точке В к профилю кулачка, t–t — касательная (рис. 16.11). Абсолютная скорость  направлена по толкателю вверх (при вращении кулачка против часовой стрелки), переносная скорость  — перпендикулярно радиусу ОВ, относительная скорость  — по касательной t–t.

Проецируя векторное уравнение (16.18) на координатные оси х, y (на рис. 16.11 показаны проекции только скорости ) и учитывая, что скорость наклонена к оси x под углом , получают алгебраические уравнения, связывающие углы давления и компоненты скорости:

                                  ,                                

                                  ,                      (16.19)

где j — угловая координата радиуса-вектора кулачка ОВ.

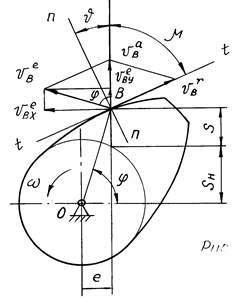
Рис. 16.11

Проекции переносной скорости на оси х, у могут быть выражены через угловую скорость кулачка и координаты точки В:

                                ,                              

                                     .                         (16.20)

где S_н — координата нижнего положения толкателя; в центральном механизме S_н = r_о.

После подстановки из (16.20) в (16.19) получают основные зависимости для определения искомых величин:

                                 ,                              

                                     .                          (16.21)

После деления выражений (16.21) на ω получают соотношения для аналогов скоростей:

                                 ,                               

                                      .                          (16.22)