Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 21

Точку d получаем на продолжении pb3, точку s3 — посередине pd. Линейные скорости:

B3 = pb3/m = 50/50 = 1 м/с; D = 70,4/50 = 1,41 м/с;         

S3 = 35/50 = 0,7 м/с; B3B2 = 56/50 = 1,12 м/с.              

Угловая скорость кулисы:

            w3 = B3C/lB3C = B3/(B3C/ml) = 1/(71/200) = –2,82 с-1.          

Направление w3 — по часовой стрелке (рис. 4.4, в).

4. Строим план скоростей диады 4–5. С диадой 2–3 ее связывает точка D, кинематика которой определена. Система векторных уравнений диады 4–5 аналогична (4.13) и примеру 4.1:

                                                                            

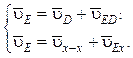
Из точки d проводим направление ED перпендикулярно DE. Из полюса p проводим направление x–x до пересечения с направлением ED в точке e. Длины отрезков:

                                  pe = 66 мм; de = 19 мм.                                

Точку s4 находим из пропорции ds4 = 0,5de = 0,5×19 = 9,5 мм. Отрезок ps4 = 68 мм. Линейные скорости:

E = 66/50 = 1,32 м/с; ED = 19/50 = 0,38 м/с;               

S4 = 68/50 = 1,36 м/с.                                 

Угловая скорость шатуна w4 = ED/lDE = 0,38/0,15 = –2,53 c-1. Направление w4 — против часовой стрелки (рис. 4.4, г).

5. План ускорений строим, также начиная с диады 2–3. Система векторных уравнений:

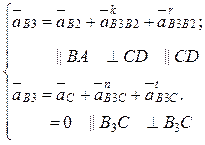                                                      (4.31)

Нормальные ускорения  и  — центростремительные, направлены к центрам вращения А и С. Векторы, известные по величине и направлению:

                        aB1 = aB2 = w12lAB = 152×0,1 = 22,5 м/с2;                     

                     = /lB3C = 12/(71/200) = 2,82 м/с2.                  

Направление кориолисова ускорения получаем поворотом вектора относительно ускорения B3B2 на 90о в сторону w3 (по часовой стрелке). Его модуль:

                    = 2w3B3B2 = 2×2,82×1,12 = 6,32 м/с2.                 

Масштаб плана ускорений ma = pb1/B1 = 90/22,5 = 4 мм/(м/с2). Длины отрезков на плане ускорений:

                            b1k = ma = 6,32×4 = 25 мм;                          

                             pn1 = ma = 2,82×4 = 11 мм.                          

Из полюса p (рис. 4.4, е) проводим вектор pb1 = 90 мм параллельно AB к точке A. Из его конца перпендикулярно BC откладываем отрезок b1k = 25 мм, из конца которого проводим направление относительного ускорения параллельно звену CD. Решая второе уравнение системы, из полюса p откладываем отрезок pn1 = 11 мм параллельно звену CD к центру вращения C. Из конца отрезка pn1 проводим направление, перпендикулярное звену CD, до пересечения с направлением  в точке b3. Полученные длины отрезков:

                                pb3 = 43 мм; n1b3 = 41 мм.                              

Точки d и s4 находим из пропорций:

                      pd = pb3CD/B3C = 43×100/71 = 60,5 мм;                    

                                   ps3 = 0,5×60,5 = 30 мм.                                 

Линейные ускорения:

                            aВЗ = πb3/μа = 43/4 = 10,45 м/с2;                          

                           = n1b3/μа = 41/4 = 10,25 м/с2;                        

                            aD = πd/μа = 60,5/4 = 15,13 м/с2;                          

                              aS3 = πs3/μа = 30/4 = 7,5 м/с2.                            

Угловое ускорение кулисы:

                   = 10,25/(71/200) = –28,87 с-2.                

Направление ε3 — по часовой стрелке (рис. 4.4, в).

6. Для построения плана ускорений диады 4–5 составляем систему векторных уравнений для диады 2-го вида, аналогичную (4.23) – (4.24):

                                                                

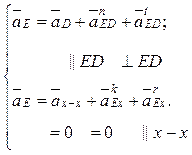
Нормальная составляющая  = /lDE = 0,382/0,15 = 0,96 м/с2.

Длина отрезка dn2 = ma = 0,96×4 = 4 мм. Из конца вектора pd откладываем отрезок dn2 = 4 мм параллельно ED в сторону точки D. Далее ему перпендикулярно проводим направление . Из полюса p проводим направление параллельно направляющей x–x. Точка пересечения направлений e определяет длины отрезков и величины векторов. Полученные длины отрезков:

Скачать файл