Учебное пособие по курсу "Теория механизмов и машин", страница 17

Относительная скорость u_CB = 7/5 = 15 м/с.

Модуль угловой скорости w₂ = u_CB / l_BC = 15/0,3 = 50 с^-1.

Направление угловой скорости определяем путем переноса вектора u_CB в точку С шатуна. Из рис. 4.1, г видно, что точка C относительно B вращается по часовой стрелке (со знаком «минус»). Следовательно, w₂ = - 50 с^-1.

Лекция № 5

4.3.3. План ускорений

Как известно из теоретической механики, ускорение точки определяют по векторному уравнению общего вида:

                                      ,                            (4.18)

где _а — абсолютное ускорение точки, м/с²; _e — переносное ускорение; _r — относительное ускорение;  — кориолисово ускорение.

Переносное и относительное ускорения при вращательном или сложном движении определяют как геометрическую сумму нормального (центростремительного) и тангенциального ускорений:

                                           .                                (4.19)

Нормальное ускорение направлено вдоль звена к центру вращения, действительному или условному, тангенциальное ускорение направлено перпендикулярно нормальному ускорению (перпендикулярно звену).

Нормальное ускорение определяют по формуле

                                  или                        (4.20)

где  — угловая скорость звена, с^-1; l — длина звена, м;  — относительная скорость, м/с.

Тангенциальное ускорение рассчитывают по формуле

                                              ,                                   (4.21)

где e — угловое ускорение звена, с^-2.

Кориолисово ускорение определяют по формуле

                                           ,                                (4.22)

где  — относительная угловая скорость;  — относительная линейная скорость в кинематической паре.

Во вращательной паре отсутствует относительная линейная скорость ( = 0), так как в идеальном шарнире совпадают центры шипа и втулки, следовательно, отсутствует и кориолисово ускорение.

В поступательной паре при известном  кориолисово ускорение в соответствии с формулой (4.22) может иметь место только при . Практически это означает наличие вращающейся направляющей (кулисы), по которой перемещается ползун (камень кулисы). Кориолисово ускорение имеет место в кулисных механизмах (см. рис. 3.13, 3.15 и 3.17), где камень кулисы скользит по качающейся или вращающейся кулисе, и отсутствует в кривошипно-ползунном механизме (рис. 4.2), где направляющая неподвижна ().

Как и при построении плана скоростей, векторные уравнения для определения ускорений составляют для внутренней кинематической пары С диады 2–3:

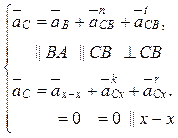
В уравнении (4.23) первое слагаемое (переносное ускорение) состоит только из нормальной составляющей, так как при постоянной заданной угловой скорости кривошипа (w₁ = const) его угловое ускорение отсутствует (e₁ = 0). Относительное ускорение a_СВ предварительно раскладывают по двум направлениям, нормальному и тангенциальному. Ускорение точки В (нормальное):

                                           .                                         

Масштаб плана ускорений, мм/(м×с^-2):

                                          ,                                (4.25)

где pb — длина отрезка, мм, изображающего ускорение а_В.

Из полюса π параллельно звену ВА в сторону точки А откладывают отрезок πb (рис. 4.1, в). Из его конца проводят параллельно СВ в сторону точки В (условно принятой за центр вращения, в индексе стоит на втором месте) вектор относительного ускорения, которое определяют по формуле (4.20):

Длина отрезка bn, изображающего нормальное ускорение,

                                           .                                 (4.26)

Если длина отрезка не превышает 2 мм, допускается на плане ускорений его не показывать. Из конца вектора bn проводят перпендикулярно ему направление тангенциального ускорения.