Реакцию ![]() находят из уравнения проекций сил:
находят из уравнения проекций сил:
![]() . (6.26)
. (6.26)
Для
нахождения второй составляющей реакции ![]() составляют
аналитическую зависимость момента силы относительно точки К с
координатами хС и уВ. Ее общее выражение
имеет вид:
составляют
аналитическую зависимость момента силы относительно точки К с
координатами хС и уВ. Ее общее выражение
имеет вид:
![]() ,
(6.27)
,
(6.27)
где X и Y — проекции силы на оси х и у; x и y — координаты точки приложения силы.
Положение точки К, не принадлежащей рассматриваемой диаде, выбирают из соображений рационального вывода аналитических соотношений. При вычислении момента силы относительно точки К используют локальные координаты с центром, расположенным в этой точке. Эти координаты определяют разностями x – xK и y – yK. С использованием этих координат и формулы (6.27) моментное уравнение равновесия диады 2–3 относительно точки К примет вид:
![]() .
. ![]()
![]()
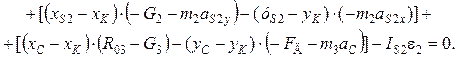 (6.28)
(6.28)
Следует заметить, что уравнение (6.28) представлено тремя парами проекций сил, приложенных в точках B, S2 и С, заключенными в квадратные скобки, и одним моментом. Координаты точек:
|
|
|
|
|
|
|
|
|
Реакцию R12y рассчитывают из уравнения (6.28), где хС – хk = 0 и уВ – уk = 0; с учетом хK = xc и yK = yB
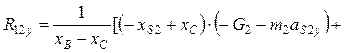
![]() . (6.29)
. (6.29)
Реакцию R03 находят из уравнения проекций сил на ось y:
![]() . (6.30)
. (6.30)
Б) Звено 3.
|
Рис. 6.19 |
Реакцию во внутренней кинематической паре диады 2–3 определяют из уравнений равновесия в проекциях на оси х и у, составленных для действующих на звено активных сил, проекций реакции и силы инерции (рис. 6.19):
![]() ;
; ![]() ; (6.31)
; (6.31)
![]()
![]() . (6.32)
. (6.32)
В) Начальный механизм.
К точке В звена 1 (рис. 6.20) прикладывают составляющие реакции, направленные противоположно составляющим R12x и R12y. Уравновешивающий момент определяют из уравнения равновесия:
![]() ;
; ![]() . (6.33)
. (6.33)
|
Рис. 6.20 |
Реакции в коренной шейке определяют из уравнений равновесия в проекциях на координатные оси:
![]() ;
; ![]() ; (6.34)
; (6.34)
![]()
![]() . (6.35)
. (6.35)
Приведенные расчетные зависимости положены в основу алгоритма силового расчета рычажного механизма ДВС по программе ТММ-1, составленной в системе Quick BASIC.
Пример 6.2. Рассчитать по данным примеров 4.1 и 6.1 аналитическими методами реакции в кинематических парах R12, R23 и R03 кривошипно-ползунного механизма (рис. 4.1, а) для 12 положений кривошипа.
Исходные
данные: угловая скорость кривошипа ω1 = 215 с-1,
угловая координата φ1 = 0…360º с шагом ![]() = 30º,
длины звеньев: lAB = 0,08 м, lBС = 0,3 м, координата центра масс шатуна lBS2
= 0,09 м; массы звеньев: m2 = 3,1 кг; m3 = 2,2 кг; момент инерции шатуна IS2 = 0,028
кг∙м2; силы, действующие на поршень, — по индикаторной диаграмме
[8].
= 30º,
длины звеньев: lAB = 0,08 м, lBС = 0,3 м, координата центра масс шатуна lBS2
= 0,09 м; массы звеньев: m2 = 3,1 кг; m3 = 2,2 кг; момент инерции шатуна IS2 = 0,028
кг∙м2; силы, действующие на поршень, — по индикаторной диаграмме
[8].
Решение:
Силовые параметры рассчитываем по программе ТММ-1. Результаты расчетов представлены на рис. 6.21.
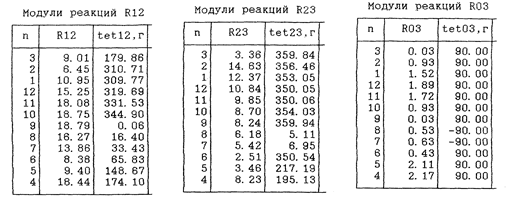
Рис. 6.21
Вывод:
Отклонение величин реакций R12 и R23 для положения 2 кривошипа составляет 5,4 % и 1,2 % соответственно. Отклонение R03 составляет — 24,7 %. Это свидетельствует о неточности графического метода, проявляющейся при малых длинах векторов.
Основы расчета диад изложены в п. 6.7.
1. На план положений диады (рис. 6.22) наносят силы
тяжести G2 и G3, силы инерции FИ2
и FИ3, моменты сил инерции МИ2 и МИ3,
момент сил сопротивления МС, направленный
против угловой скорости, и составляющие реакций ![]() и
и ![]() ,
, ![]() и
и ![]() . Искомыми являются реакции в
кинематических парах R12, R23 и R03.
Проведя линии действия сил G и FИ, опускают на них из
точки С перпендикуляры, длины которых hi являются плечами сил.
. Искомыми являются реакции в
кинематических парах R12, R23 и R03.
Проведя линии действия сил G и FИ, опускают на них из
точки С перпендикуляры, длины которых hi являются плечами сил.
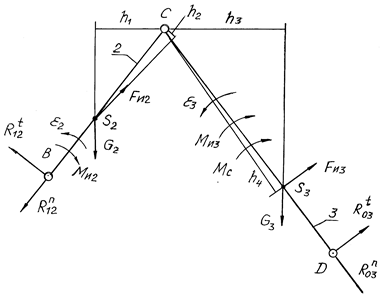
Рис. 6.22
2. Аналитическое уравнение моментов для звена 2:
![]() ;
; ![]() . (6.36)
. (6.36)
Из уравнения
(6.36) находят составляющую ![]() .
.
3. Моментное уравнение для звена 3:
![]() ;
; ![]() .
(6.37)
.
(6.37)
Из уравнения
(6.37) находят составляющую ![]() .
.
4. Векторное
уравнение для диады 2–3 с двумя искомыми векторами![]() и
и![]() , известными по
направлению:
, известными по
направлению:
![]() . (6.38)
. (6.38)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.