Учебное пособие по курсу "Теория механизмов и машин", страница 76

                                       ,                                      где h — КПД одной ступени зубчатой передачи [20]: h = 0,95 … 0,97.

Крутящие моменты на колесах и соответствующих валах связаны с передаточными отношениями и КПД по формуле (12.5).

Момент на водиле:

                                           .                                 (13.9)

Момент на солнечном колесе:

                                           .                               (13.10)

Момент на сателлите:

                                           .                               (13.11)

Пример 13.1. Рассчитать передаточное отношение редуктора Джеймса (см. рис. 13.1), угловые скорости валов и крутящие моменты на валах по следующим исходным данным: числа зубьев колес z₁ = 20; z₂ = 31; z₃ = 82; момент на валу солнечного колеса Т₁ = 50 Н×м; угловая скорость этого вала  = 40 с^-1; КПД одной ступени h = 0,96.

Решение:

1. Передаточное отношение от солнечного колеса к водилу

                                     .                                   

2. Коэффициент полезного действия механизма — формула (13.7):

                            .                         

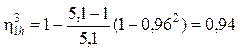3. Угловые скорости звеньев:

                             ;                          

                            .                         

4. Моменты на валах:

                            Т₂ = 50×(31/20)×0,96 = 74,4 Н×м;                          

                          Т₃ = 50×(82/20)×0,96² = 188,93 Н×м;                        

                              Т_h = 50×5,1×0,94 = 239,7 Н×м.                            

Выводы:

1. КПД планетарного редуктора выше, чем двухступенчатой рядовой передачи (0,96² = 0,92).

2. Угловая скорость водила имеет положительный знак, сателлита — отрицательный. Это означает, что солнечное колесо и водило вращаются в одну и ту же сторону, что подтверждает формулу (13.3), а сателлит — в противоположную.

Редуктор Джеймса — самый распространенный планетарный механизм. Он сравнительно прост в изготовлении, имеет малые осевые габариты и в два раза меньшую массу, чем рядовая передача. Он работает в интервале передаточных отношений  с высоким коэффициентом полезного действия (до 0,98). Число сателлитов чаще всего n_c = 3 (до n_c = 6). Он используется в силовых передачах в виде отдельных устройств — редукторов, мотор-редукторов, а также конструкций, встроенных в колесо, звездочку либо в барабан лебедки и другие устройства.

13.1.2. Редукторы Давида

В технике используются самые разнообразные схемы планетарных редукторов. Далее рассмотрим некоторые из них.

Редуктор Давида и его модификации имеют сдвоенные сателлиты z₂ – (рис. 13.2), которые так же, как и в редукторе Джеймса, входят в два зацепления: z₁/z₂ и /z₃. В базовой модификации оба зацепления — внешние. Такой механизм также называется эпициклическим. Он относится к классу 2k – h. Обычно в редукторе Давида ведущее звено — водило h. При этом формула Виллиса может быть использована только после инверсии:

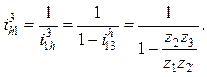                                                   (13.12)

Так как соотношения чисел зубьев могут быть различными, знак  может быть как плюс, так и минус. Кроме того, если подобрать так числа зубьев, чтобы отношение их было близко к единице, то передаточное отношение может быть весьма значительным.

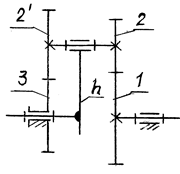
Рис. 13.2

Пример 13.2. Рассчитать передаточное отношение редуктора Давида при числах зубьев: z₁ = 100; z₂ = 101;  = 100; z₃ = 99.

Решение:

Передаточное отношение от водила к солнечному колесу 1:

                       .                     

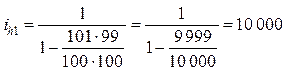Для получения такого передаточного отношения потребовалось бы 12 зубчатых колес рядовой передачи. Однако такие редукторы имеют КПД меньше одного процента и в силовых передачах не используются.

Меньшие потери и более высокий КПД будет в модификации редуктора Давида с двумя внутренними зацеплениями (гипоциклический механизм, рис. 13.3). Его передаточное отношение определяют по формуле (13.12). Он так же, как и эпициклический механизм, применяется в кинематических передачах.