Учебное пособие по курсу "Теория механизмов и машин", страница 22

                         ps₄ = 65 мм; n₂e = 1 мм; pe = 65 мм.                      

Линейные ускорения:

                  a_E = 65/4 = 16,25 м/с²; a_S4 = 65/4 = 16,25 м/с²;                

                                    = 1/4 = 0,25 м/с².                                 

Угловое ускорение шатуна

         e₄ = /l_ED = 0,25/0,15 = –1,67 с^-2 (по часовой стрелке).       

Замечание. В связи с очень близкими расстояниями между точками n₂, e и s₄ значения  и e₄, полученные методом планов, могут оказаться существенно искаженными. На рис. 4.4, е фрагмент плана ускорений с этими точками изображен в увеличенном масштабе.

4.3.6. Структурный и кинематический анализ механизма с качающимся цилиндром^*

Такой механизм нашел широкое применение в строительных и путевых машинах, в подвижном составе и во многих других устройствах.

Пример 4.5. В коромыслово-кулисном механизме (рис. 4.5, а) задано: длина коромысла l₃ = 0,1 м; угловой ход (размах) коромысла b = 60°; конструктивный коэффициент k = 1,4.

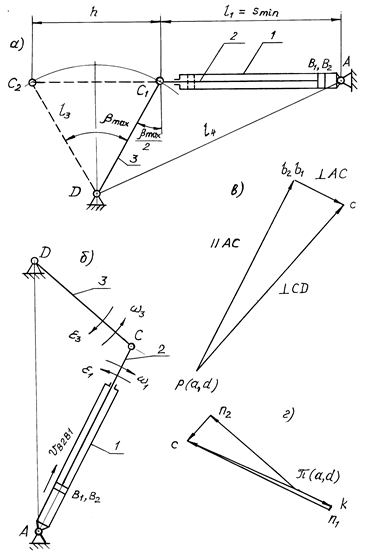
Рис. 4.5

Спроектировать механизм по минимальному углу давления, определив длины цилиндра s и стойки l₄.

Выполнить кинематический анализ механизма, приняв постоянную скорость перемещения поршня _B2B1 = 0, 1 м/с и длину цилиндра s — по результатам синтеза.

Определить скорость и ускорение точки C, угловые скорости и ускорения w₁ и w₃, e₁ и e₃.

Решение:

1. Синтез коромыслово-кулисного механизма (рис. 4.5, а) выполняем по теме 10 настоящего издания. Ход поршня — по формуле (10.28):

                      h = 2l₃×sin(b/2) = 2×0,1×sin(60/2) = 0,1 м.                    

Принимаем стандартное значение h = 100 мм = 0,1 м.

Минимальная длина цилиндра l₁:

                             s_min = l₁ = kh = 1,4×0,1 = 0,14 м.                          

Максимальная длина

                          s_max = s_min + h = 0,14 + 0,1 = 0,24 м.                       

Для полного исследования необходимо задавать s = 0,14…0,24 м с некоторым шагом, например, 0,01 м. В данном примере принимаем s = 0,16 м.

Длину стойки находим из DAC₁D по теореме косинусов:

                =м.              

Принимаем l₄ = 0,21 м.

2. Вычерчиваем план положений (рис. 4.5, б) в масштабе m_l = = DC/l₃ = 60/0,1 = 600 мм/м. Длина отрезка AD, изображающего стойку, равна l₄/m_l = 0,21×600 = 126 мм. Откладываем длину AD = = 126 мм по вертикали, расположив точку A под точкой D. Положение точки C определим методом засечек. Для этого проводим две дуги окружности с радиусами DC = 60 мм и AC = sm_l = = 0,16×600 = 96 мм до их пересечения.

3. Система векторных уравнений для построения плана скоростей:

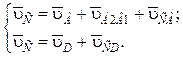                                                          (4.32)

Масштаб плана скоростей m== 100/0,1 = 1000 мм/(м×с^-1). Вектор pb₂ = 100 мм проводим параллельно AC (рис. 4.5, в). Из его конца проводим направление _CA перпендикулярно AC. Из полюса p проводим направление _CD, перпендикулярное CD. В искомую точку c проводим стрелки. Длины отрезков на плане скоростей:

                                 pc = 103 мм; b₂c = 26 мм.                               

Величины относительных скоростей:

_CD = pc/m = 103/1000 = 0,103 м/с;                      

_CA = 26/1000 = 0,026 м/с.                              

Угловые скорости звеньев:

                    w₁ = w₂ = _CA/l_AC = 0,026/0,16 = –0,163 с^-1;                  

                          w₃ = _CD/l_CD = 0,103/0,1 = 1,03 с^-1.                        

Направление угловых скоростей определяем, прикладывая векторы _CA и _CD в точку C плана положений. Направление w₁ — отрицательное (по часовой стрелке), w₃ — положительное (против часовой стрелки).

4. Система векторных уравнений для построения плана ускорений:

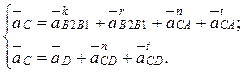                                              (4.33)

Кориолисово ускорение  = 2w_1B2B1 = 2×0,163×0,1 = 0,033 м/с². Относительное ускорение  = 0, так как скорость движения штока 2 относительно цилиндра 1 постоянна. Ускорение a_D = 0, так как точка D неподвижна. Модули нормальных ускорений:

                     = /l_AC = 0,026²/0,16 = 0,0042 м/с²;