Известно, что при установившемся движении рычажного механизма скорость w1 начального звена меняется во времени (тема 8, график XI на рис. 8.3, г). В соответствии с формулой динамики (NB 8.1) появляется угловое ускорение e1, которое, так же как и wI, меняется циклически. Так же переменны кинематические параметры других звеньев механизма, совершающих сложное движение (шатун) и возвратно-поступательное движение (поршень). Вследствие этого звенья подвергаются воздействию динамических усилий (FИ и MИ), а в кинематических парах механизма возникает динамическое давление, которое передается на стойку.
Под действием динамических давлений стойка во время работы механизма колеблется (вибрирует), а вместе с ней вибрирует и его фундамент. Крепления стойки с фундаментом должны быть достаточно надежными, а фундамент — массивным. Это удорожает всю установку. Поэтому всегда принимают меры для разгрузки станины и фундамента от динамических усилий. Этого можно добиться таким распределением масс звеньев механизма, при котором
(9.1)
(9.2)
где 
—
главный вектор сил инерции; это векторная сумма сил инерции; 
— главный момент сил инерции.
NB 9.1. Разгрузки станины и фундамента от динамических усилий можно добиться таким распределением масс звеньев механизма, при котором главный вектор сил инерции и главный момент сил инерции равны нулю в любой момент движения.
В процессе динамических расчетов силы FИ и моменты сил инерции MИ прикладывают к звеньям механизма в соответствии с принципом Даламбера. Как известно, на звенья механизмов действуют внешние силы (сопротивления FС и тяжести G). Однако в сравнении с силами инерции они зачастую настолько малы, что ими можно пренебречь. Это можно проиллюстрировать примером.
Пример 9.1. Определить силу инерции маховика с массой m = = 10 кг, вращающегося с угловой скоростью w = 1000 рад/с (частотой вращения n = 9550 об/мин), если расстояние от центра его тяжести до оси вращения rs = 0,0001 м (0,1 мм).
Решение:
Силa инерции звена
10×10002×0,0001 = 1000 Н.
Вес звена
G = mg = 9,81×10 = 98,1 Н.
Вывод:
Таким образом, при очень малом смещении центра масс (всего в 0,1 мм) сила инерции превосходит вес приблизительно в 10 раз.
Скорости некоторых современных машин сопоставимы с приведенной в примере. Так, автомобильные двигатели имеют частоты вращения n £ 5 000 об/мин, электродвигатели и турбовинтовые двигатели — до n = 20 000 об/мин, центрифуги — до n = = 50 000 об/мин. При таких частотах вращения силы инерции достигают больших величин. Они в отличие от сил тяжести имеют переменные направления. Возникающие при этом динамические реакции также переменны и могут вызвать нежелательные колебания звеньев механизма. Таким образом, главная задача уравновешивания — уравновешивание сил инерции.
В теории уравновешивания ротором называют любое вращающееся звено (рабочее колесо турбины, якорь электродвигателя, коленчатый вал, шлифовальный круг и т.д.).
При невыполнении условий (9.1) и (9.2) звено является неуравновешенным. Для уравновешивания вращающегося звена, имеющего небольшие осевые размеры (шкив, маховик, шлифовальный круг и т.п.), достаточно выполнения только условия (9.1), которое записывают так:
(9.3)
где rs —
эксцентриситет массы звена, м; это расстояние от центра тяжести звена до центра
вращения; 
— главный вектор дисбалансов звена, кг×м (г×мм),
(9.4)
S — статический момент, кг×м.
Если рассматривать вращающееся звено, состоящее из n-го числа элементарных масс mi, удаленных на расстояния ri от оси вращения, то главный вектор дисбалансов будет равен:
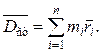(9.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.