Учебное пособие по курсу "Теория механизмов и машин", страница 107

5. Ограничения по числам зубьев осуществляют вводом z_min = = 17; z_max = 150 (или 200). Вначале принимают z₂ = z_min. Компьютер рассчитывает числа зубьев и проверяет условия z₁ ³ z_min и z₃ £ z_max. В дальнейшем величину z₂ увеличивают на единицу. Пределом является z₂ = z_max.

6. Проверку условий соседства, сборки и правильного зацепления выполняют в соответствии с п. 15.2.

7. Оптимизация по габаритам редуктора. Основной критерий оптимизации — минимальные габариты редуктора, связанные с числом зубьев корончатого колеса z₃. В каждом цикле расчета записываются в памяти ПЭВМ числа зубьев z₃ и заменяются только при выполнении условия

                                         (z₃) _n < (z₃) _n-1.                                       

После перебора чисел зубьев z₂ в интервале z_min и z_max и выполнения всех условий числа зубьев z₁, z₂ и z₃ выводятся на печать.

8. Для оптимального варианта рассчитывается механический КПД по формуле (13.7).

9. При составлении программы учтено, что при z₁ = z_min = 17 и z₂ = 19 (см. табл. 14.1) в соответствии с формулой (15.21) d ³ 36, поэтому варианты с d < 36 компьютер не рассматривает. Блок-схема алгоритма расчета чисел зубьев редуктора Джеймса приведена в методике [21].

Пример 15.3. Рассчитать на ПЭВМ числа зубьев z₁, z₂, z₃ и КПД редуктора Джеймса (см. рис. 15.1) по исходным данным примера 15.1:  = 6,5; n_с = 3; h = 0,96.

Решение:

По программе ТМ22 находим числа зубьев и КПД. Распечатка результатов расчета приведена на рис. 15.4.

Рис. 15.4

Вывод:

Компьютерные расчеты дают меньшие габариты передачи, чем в примере 15.1 (z₃ = 96 против 132). При этом обеспечена точность Di = 2,56 % при допуске в 4 %.

Б. Эпигипоциклический механизм.

1. Условие соосности — по формуле (15.17):

                                        z₁ + z₂ = z₃ – z₂¢                                                                 

или

                                     z₃ – z₁ = z₂ + z₂¢ = d,                                    откуда

                                            z₁ = z₃ – d;                                (15.25)

                                            z₂ = d – z₂.                                (15.26)

2. Из кинематического условия (13.13), формул (15.25) и (15.26) находят d:

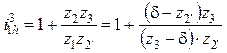                             ,                            откуда

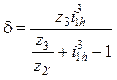                                        .                            (15.27)

3. Задают максимальные числа зубьев , при которых рассчитывают z₁ и z₂ по формулам (15.25) и (15.26) при изменении параметра d в целых числах в пределах d_min – d_max. Условия и ограничения синтеза аналогичны описанным для редуктора Джеймса. В последующих циклах расчета числа зубьев уменьшают на единицу и расчеты продолжают до z₁ = z_min и  = 19.

4. Параметром оптимизации является условный радиальный габарит d_i, равный либо z₃/2, либо z₁/2 + z₂. КПД передачи рассчитывают по формуле (13.7). Блок-схема алгоритма приведена на рис. 15.5.

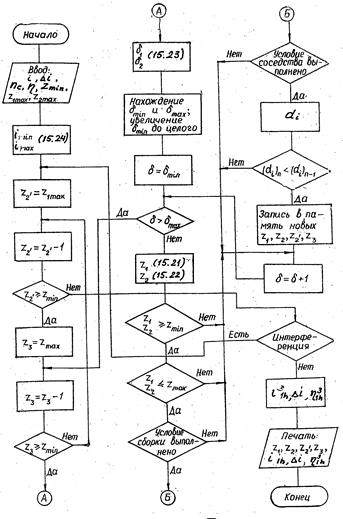
Рис. 15.5

Пример 15.4. Рассчитать на ПЭВМ числа зубьев эпигипоциклического механизма z₁, z₂,  и z₃ и КПД  по исходным данным примера 15.2:  = 14,5; n_c = 3; h = 0,96.

Решение:

По программе ТМ22 находим числа зубьев и КПД. Распечатка результатов расчетов приведена на рис. 15.6.

Рис. 15.6

Проверки:

1) 17 + 62 = 110 – 31; 79 = 79;

2)  = 1 + 62 × 110/(17×31) = 13,94;

3) (17 + 62) sin(180/3) – 62 = 6,42 > 2;

(110 – 31) sin(180/3) – 31 = 37,4 > 2;

4) g = 17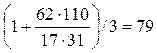 — целое число;

5) интерференции нет.

Выводы:

1. Все условия выполнены.

2. Отклонение Di = 3,9 % < 4 %.

3. Компьютерные расчеты дали меньшие размеры, чем в примере 15.2: условный габарит z₁/2 + z₂ = 17/2 + 62 = 70,5 против 24/2 + 63 = 75.

15.5. Табличный метод выбора чисел зубьев

Для сложных схем планетарных механизмов подбор чисел зубьев оказывается весьма трудоемкой операцией. Для таких схем, в частности, для схемы 3k со сдвоенным сателлитом (см. рис. 13.7), предварительно рассчитанные числа зубьев сведены в таблицы [18]. Фрагмент одной из них приведен в табл. 15.1.