Учебное пособие по курсу "Теория механизмов и машин", страница 38

где k — число поступательных кинематических пар; m — число вращательных пар; R_п — реакция в поступательной паре, Н; например, R₀₃; R_в — реакция во вращательной паре, Н (R₀₁, R₁₂, R₂₃); f_п — коэффициент трения в поступательной паре, рекомендуется f_п = 0,1; f_в — коэффициент трения во вращательной паре (f_в = 0,08); _r — относительная скорость в поступательной паре, м/с; например, υ_С; ω_r — относительная угловая скорость, с^-1, определяется с учетом знаков угловых скоростей ω_i и ω_j соседних звеньев по формуле

                                          ω_r = | ω_i – ω_j|,                                (6.22)

r — радиус шарнира; определяется ориентировочно из формулы расчета на износостойкость по давлению:

                                                                          (6.23)

с округлением до стандартного по ГОСТ 6636-69.

Мощности — величины переменные. Для каждого положения начального звена мгновенная мощность:

                                         Р_мгн = Р₁ ± Р_Т.                              (6.24)

Знак «плюс» берут для технологических машин, знак «минус» — для двигателей. Механический КПД — величина, всегда меньшая единицы; определяется по формулам соответственно для двигателей и технологических машин:

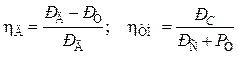                            .                 (6.25)

6.10. Заключение по силовому расчету диады 2-го вида

1. Цель силового расчета — определение реакций в кинематических парах, мощностей и КПД.

2. Силовой расчет можно проводить не только для одного звена, но и для нескольких звеньев, составляющих группу Ассура, которая является кинетостатически определимой.

3. Последовательность расчетов может быть разной, однако их необходимо вести наиболее рациональным способом.

4. Силовой расчет группы Ассура, состоящей из двух звеньев, является единственно возможным способом, так как при расчете звеньев 2 и 3 по отдельности число неизвестных будет больше числа уравнений.

5. Векторные уравнения решаются либо пересечением двух известных векторов, либо замыканием векторного многоугольника.

6. Найденные в результате силового расчета реакции могут быть использованы:

– для определения мощностей и КПД;

– для расчета звеньев на прочность и жесткость;

– для расчета шарниров на износостойкость.

Пример 6.1. Рассчитать по данным примеров 4.1 и 5.2 реакции R₀₃, R₃₂, R₁₂ и R₀₁ в кинематических парах кривошипно-ползунного механизма (см. рис. 4.1, а), мощности и КПД.

Исходные данные: угловая скорость кривошипа ω₁ = 215 с^-1, угловая координата φ₁ = 30º, длины звеньев — l_AB = 0,08 м, l_BС = 0,3 м, координата центра масс шатуна l_BS2 = 0,09 м; массы звеньев — m₁ = = 38 кг; m₂ = 3,1 кг; m₃ = 2,2 кг; момент инерции шатуна I_S2 = = 0,028 кг∙м²; движущая сила F_д = 22777 Н.

Из решения примера 5.2 кинематические параметры заданного механизма: угловая скорость шатуна ω₂ = –50,1 с^-1; угловое ускорение шатуна ε₂ = 5881 с^-2; скорость и ускорение ползуна — _С = = –10,6 м/с; а_С = –3713 м/с²; ускорение центра масс шатуна а_S2 = = 3597 м/с².

Решение:

1. Вес звеньев (всегда направлен вертикально вниз):

           G₁ = m₁g = 38 ∙ 9,81 = 373 Н; G₂ = 3,1 ∙ 9,81 = 30,4 Н;         

                                  G₃ = 2,2 ∙ 9,81 = 21,6 Н.                                

2. Силы инерции звеньев (направлены против векторов ускорений центров масс звеньев):

     F_И2 = m₂a_S2 = 3,1 ∙ 3597 = 11151 Н; F_И3 = 2,2 ∙ 3713 = 8169 Н.   

3. Момент сил инерции шатуна (направлен против углового ускорения):

                     М_И2 = –I_S2ε₂ = –0,028 ∙ 5881 = –165 Н∙м.                   

4. Составляем расчетную схему (см. рис. 6.12). Прикладываем в точке В искомые реакции  и , в точке S₂ — известные силы G₂ и F_И2, в точке С — известные силы F_Д, F_И3, G₃ и реакцию искомую R₀₃, на звене 2 — момент М_И2. Длины отрезков в масштабе m_l = 400 мм/м (см. пример 4.1): ВС = 120 мм; h₁ = 42 мм; h₂ = 83 мм.

5. Составляем уравнение моментов относительно точки С — формула (6.11), из которой находим искомую реакцию:

           = (–11151 ∙ 42 + 30,4 ∙ 83 – 165 ∙ 400)/120 = –4432 Н.