Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 27

Параметр

Вариант

1

2

3

Положение кривошипа

10

7

5

Угловая скорость w1, с-1

24

–36

-50

Длины звеньев:                  lАВ, м

0,3

0,6

0,9

                                           lВС, м

0,4

0,8

1,1

                                          lCD, м

0,5

1,4

1,3

                                           lAD, м

0,5

1,2

1,0

Координаты центров масс: lBS2, м

0,25

0,2

0,4

                                           lCS3, м

0,15

0,5

0,3

Задача № 19 (рис. 4.11) [9]

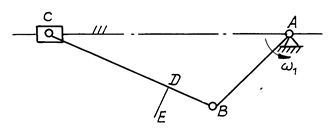
Рис. 4.11

Построить в выбранных масштабах и заданном положении кривошипа планы положений, скоростей и ускорений кривошипно-ползунного механизма. Определить величины и направления: B, E в м/с,  в м/с2, e2 в с-2.

Параметр

Вариант

1

2

3

Положение кривошипа

7

2

10

Угловая скорость w1, с-1

15

–25

–30

Длины звеньев: lАВ, м

0,1

0,25

0,3

                           lВС, м

0,3

0,75

0,8

                           lBD, м

0,1

0,15

0,2

                           lED, м

0,1

0,2

0,3

Задача № 22 (рис. 4.12) [9]

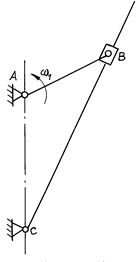
Рис. 4.12

Построить в выбранных масштабах и заданном положении кривошипа планы положений, скоростей и ускорений кривошипно-кулисного механизма. Определить величины и направления: B1, B3, B3B2 в м/с,  в м/с2, e3 в с-2.

Параметр

Вариант

1

2

3

Положение кривошипа

2

7

11

Угловая скорость w1, с-1

55

–60

80

Длины звеньев: lАВ, м

0,1

0,2

0,3

                           lAС, м

0,25

0,5

0,7

                          lCD, м

0,4

0,8

1,2

Лекция № 6

Тема 5: Аналитические методы кинематического анализа

5.1. Общие сведения

Рассмотренные в теме 4 графические методы наглядны и в некоторых случаях просты, но точность полученных результатов не всегда достаточна. Этот недостаток практически отсутствует при определении кинематических параметров аналитическими методами. Сущность методов заключается в том, что координаты, скорости и ускорения определяют в виде аналитических выражений, которые содержат конечное число алгебраических или тригонометрических операций.

NB 5.1. Основные методы определения аналитических выражений — векторный и координатный.

Исходными данными являются кинематическая схема механизма, определяющая его структуру; размеры звеньев; угловая скорость начального звена и зависимости обобщенных координат механизма от времени. Для иллюстрации аналитических методов рассматривается определение кинематических параметров диадных механизмов.

Цель темы — изучение методов составления аналитических выражений для определения кинематических параметров звеньев и отдельных точек механизма: координат, перемещений, направляющих углов, линейных и угловых скоростей точек, линейных и угловых ускорений звеньев при заданных их длинах, угловой скорости и положения начального звена.

5.2. Синусный механизм

Рис. 5.1

Синусный механизм (кулиса Вольфа) состоит из начального звена 1 и диады 5-го вида (рис. 5.1). Заданы: длина кривошипа l1 = lAB и угловая скорость w1. Определить скорость и ускорение кулисы C.

Положение точки C определяют линейной координатой хC, а угловую координату кривошипа j1 отсчитывают от оси y в направлении по часовой стрелке.

                                          .                                 (5.1)

Скачать файл