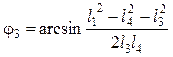Учебное пособие по курсу "Теория механизмов и машин", страница 33

                                  .                       (5.80)

Для определения угловых скоростей ω₁ и ω₃ дифференцируют уравнения (5.75) и (5.76) по обобщенной координате l₁. В результате получают выражения:

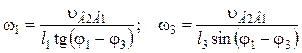                     .          (5.81)

Пример 5.4. Рассчитать аналитическим методом направляющие углы и угловые скорости звеньев коромыслово-кулисного механизма по исходным данным и решению примера 4.5: длины звеньев: l₃ = 0,1 м; l₄ = 0,21 м; линейная координата l₁ = 0,16 м. Скорость перемещения поршня υ_B2B1 = 0,1 м/с.

Решение:

Направляющий угол коромысла — формула (5.80):

                     .                   

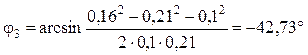Направляющий угол цилиндра — формула (5.77):

               .            

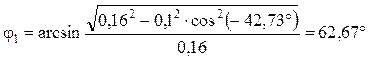Угловые скорости звеньев — формулы (5.81):

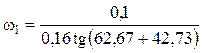                       = – 0,172 с^-1;                   

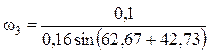                       = 1,037 с^-1.                    

Анализ. Расхождения со значениями ω₁ и ω₃, рассчитанными в примере 4.5 (–0,163 и 1,03), составляют 5,2 % и 0,7 % соответственно, что допустимо.

Ключевые положения

1. Аналитические методы кинематического анализа заключаются в определении кинематических параметров с помощью предварительно выведенных аналитических выражений.

2. Скорости или их составляющие определяются по аналитическим зависимостям, полученным дифференцированием выражения перемещений или координат положения точки (координатный метод).

3. Метод замкнутых векторных контуров (векторный метод) заключается в том, что рычажные звенья заменяют соответствующими векторами, для которых составляют и решают векторные уравнения.

4. Положительное направление векторов — вдоль осей х и у, угловые координаты (направляющие углы) отсчитывают от положительного направления оси х против часовой стрелки, положительное направление угловых параметров — против часовой стрелки.

5. Направляющие углы определяют из системы аналитических уравнений, полученных проецированием векторного уравнения на координатные оси.

6. Угловые скорости определяют путем решения системы аналитических уравнений проекций первых производных по времени.

7. Угловые ускорения определяют путем повторного дифференцирования уравнений проекций.

8. Для определения параметров центра масс шатуна используют координатный метод: составляют уравнения координат точки, затем их дифференцируют, получая уравнения проекций скоростей на координатные оси, повторное дифференцирование дает уравнение проекций ускорений, полные скорости и ускорения определяют геометрическим суммированием.

Обозначения и термины

, … — длины векторов, совмещенных с рычажными звеньями, мм;

φ₁, φ₂ — направляющие углы векторов, град;

l_b — длина базового вектора, м;

х и y — координаты точек, м;

λ — коэффициент длины;

D — определитель;

θ — угол вектора относительно оси х, град, рад.

Вопросы, выносимые на экзамен

1. Аналитические методы кинематического исследования. Синусный механизм.

2. Кинематическое исследование шарнирного четырехзвенника аналитическим способом. Метод замкнутых векторных контуров.

3. Кинематическое исследование шарнирного четырехзвенника аналитическим способом. Определение параметров центра масс шатуна.

4. Блок-схема алгоритма кинематического исследования шарнирного четырехзвенника аналитическим способом.

Лекция № 7

Тема 6: Кинетостатический анализ механизмов

6.1. Задачи динамического исследования

При кинематическом анализе исследование движения механизма проводят с учетом структуры и геометрических характеристик звеньев, но без учета силовых характеристик, приложенных к звеньям, изменяющихся по величине и направлению. Основными задачами динамики механизмов и машин являются:

1) определение реакций в кинематических парах механизма и уравновешивающего момента;

2) определение мощности сил сопротивления, сил трения, движущих сил и механического КПД;

3) определение закона движения механизма, находящегося под действием определенных сил;

4) выявление условий, обеспечивающих заданный закон движения механизма;

5) уравновешивание звеньев и механизмов.