При назначении чисел зубьев необходимо учитывать ряд ограничений:
а) числа зубьев должны быть целыми числами;
б) выбранные числа зубьев должны давать передаточное отношение i с допустимой точностью Di; по ГОСТ 2185-66 при i ³ 3,5 Di = ±4 %;
в) рекомендуется для большинства случаев использовать нулевые прямозубые колеса с ограничениями для колес с наружными зубьями по минимально допустимым числам зубьев из условия неподрезания — zн. min = 17, для колес с внутренними зубьями из условия отсутствия интерференции — zв. min = 19 (см. табл. 14.2).
Другие ограничения рассмотрены ниже.
Условия синтеза рассмотрены в основном на примере простого планетарного механизма (редуктор Джеймса, рис. 15.1). Механизм имеет два зацепления: внешнее z1/z2 и внутреннее z2/z3. Редукторы Давида с двухвенцовыми сателлитами типа 2k-h также имеют два зацепления (см. рис. 13.2–13.5).
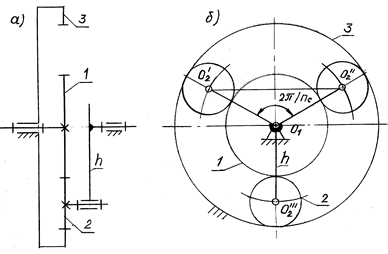
Рис. 15.1
1. Условие соосности предполагает равенство межосевых расстояний обоих зацеплений, так как оси центральных колес совпадают:
а12 = а32 или r1 + r2 = r3 – r2.
Так как r = mz/2, можно записать:
z1 + z2 = z3 – z2, (15.1)
откуда
z2 = (z3 – z1)/2. (15.2)
2. Кинематическое условие, выраженное через числа зубьев, — формула (13.3):
, откуда
z3
= (
– 1) z1. (15.3)
При точности Di = 0 подбор чисел зубьев можно вести в такой последовательности:
а) задаваясь z1 = 17, 18 и т.д., находят z3 по формуле (15.3);
б) рассчитывают z2 из условия соосности — формула (15.2);
в) выполняют проверки по следующим трем условиям.
3. Условие
соседства предполагает отсутствие интерференции зубьев соседних сателлитов.
Для этого необходимо, чтобы расстояние между осями соседних сателлитов 
(рис. 15.1, б) было больше диаметра
вершин сателлитов da2 (двух радиусов 2ra2).
Из D
следует:
2 (r1 + r2) sin (p/nc) > 2ra2 = m (z2 + 2) или
(z1 + z2) sin (p/nc) – z2 > 2. (15.4)
|
Рис. 15.2 |
При числе сателлитов nc £ 3 условие соседства всегда выполняется. Недопустимая по условию соседства ситуация показана на рис. 15.2.
4. Условие сборки предполагает отсутствие интерференции зубьев сателлитов с зубьями центральных колес.
Правильная сборка характеризуется тем, что центральные углы между межосевыми линиями соседних сателлитов одинаковы и равны 2p/nc (см. рис. 15.1, б), т.е. обеспечивается симметрия зон зацепления.
|
Рис. 15.3 |
После установки первого сателлита подвижное центральное колесо 1 займет строго определенное положение. При невыполнении условия сборки при установке других сателлитов их зубья не окажутся точно против впадин центральных колес и осуществить сборку колес будет невозможно (рис. 15.3).
Для вывода условия сборки рассмотрим схему (см.
рис. 15.1, б). Сателлит с осью 
ставится
на вертикальную ось. Затем водило поворачиваем по часовой стрелке на угол
jh = 2p/nc + 2pn, (15.5)
где n — число полных поворотов водила.
При этом
колесо 1 повернется на угол 
и займет положение 
. Далее ставят второй сателлит на свою ось
, находящуюся теперь в том месте, которое
занимал сателлит с осью 
до поворота водила. Но
при одинаковых сателлитах второй сателлит войдет на свое место только тогда,
когда сцепляющееся с ним солнечное колесо 1 повернется на целое число
угловых шагов g (на целое число
зубьев), т.е. когда
j1 = g2p/z1, (15.6)
где g — любое целое число. С учетом (15.5) и (15.6) записываем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
