Выбор оптимального варианта механизма с наилучшим приближением к заданному закону движения — сложная задача. На процесс синтеза влияет вид кинематической пары. Ниже рассмотрены методики проектирования диадных механизмов, содержащих низшие кинематические пары. Синтез зубчатых механизмов, содержащих высшие пары, рассмотрен в теме 14, кулачковых механизмов — в теме 16.
Проектирование рычажных механизмов содержит следующие этапы:
1. Проектирование схемы механизма (этой цели служит структурный синтез механизма).
2. Установление основных размеров, что и является задачей синтеза.
3. Конструктивное оформление.
4. Кинематический и динамический анализ.
5. Расчет звеньев на прочность, жесткость, износостойкость и по другим критериям.
NB 10.1. Определение основных размеров звеньев механизма по заданным его свойствам называется метрическим синтезом механизма.
Важной кинематической характеристикой при синтезе механизма является проворачиваемость его звеньев, т.е. наличие в нем одного или двух кривошипов. Она зависит от соотношения длин звеньев. Рассмотрим плоский шарнирный четырехзвенник ABCD (рис. 10.1). Заданы l1, l2, l3 и l4 — длины звеньев, причем для исследования вариантов длин стойки принимают:
l1 < l2 < l3 < l4. (10.1)
Для того, чтобы звено АВ было кривошипом, оно должно при вращении последовательно пройти через крайние левое (АВ1) и правое (АВ2) положения. На рис. 10.1 шарнирный четырехзвенник показан в двух крайних положениях совпадения кривошипа и стойки: штриховыми линиями — крайнее левое положение, штрихпунктирными — крайнее правое. Линиями видимого контура показано произвольное положение механизма. Из DВ1С1D следует:
![]() , (10.2)
, (10.2)
из DВ2С2D:
![]() . (10.3)
. (10.3)
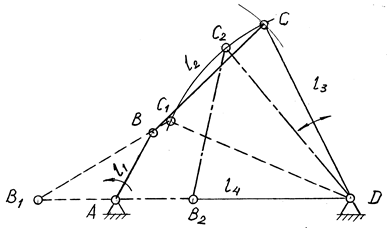
Рис. 10.1
Независимо от соотношения длин l2 и l3 неравенство (10.2) всегда обеспечит выполнение неравенства (10.3). Позиции AB1 и AB2 характеризуют крайние положения звена 1, которое будет кривошипом, т.е. звеном, совершающим полный оборот. Позиции DC1 и DC2 свидетельствуют о том, что звено CD не совершает полного оборота. Оно совершает качательное движение и называется коромыслом. Механизм с данными свойствами называется кривошипно-коромысловым. Неравенство (10.2) характеризуется правилом Грасгофа, которое можно записать следующим образом.
NB 10.2. Правило Грасгофа:
Для существования кривошипа в шарнирном четырехзвеннике необходимо, чтобы сумма длин кривошипа и стойки была меньше суммы длин двух других звеньев.
Применяя правило Грасгофа, шарнирные четырехзвенники разбивают на три группы. Для анализа всех возможных соотношений между длинами звеньев четырехзвенника используют постановку механизма на разные звенья.
1. В исходном базовом положении ABCD (см. рис. 10.1) четырехзвенник поставлен на звено 4. Правило Грасгофа выполняется для звена 1, так как условие (10.2) записано для него и оно является кривошипом. Проверка проворачиваемости звена 3 дает отрицательный результат:
l3 + l4
![]() l1 + l2.
l1 + l2.
Звено 3 может совершать только качательное движение и является коромыслом, а сам механизм — кривошипно-коромысловым.
2. При постановке механизма на звено 1 (рис. 10.2) условие (10.2) выполняется для звеньев 2 и 4, т.е. механизм будет двухкривошипным. Это следует из условий:
l2 + l1 < l3 + l4; звено 2 — кривошип;
l4 + l1 < l2 + l3; звено 4 — тоже кривошип.
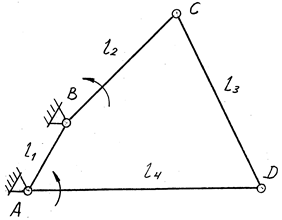
Рис. 10.2
Заметим, что стойка — самое короткое звено.
3. При постановке четырехзвенника на звено 2 (рис. 10.3) условие (10.2) выполняется для звена 1 (кривошип) и не выполняется для звена 3 (коромысло). Проверка проворачиваемости звеньев дает такие неравенства:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.