Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 13

Рис. 3.35

Рис. 3.36

Рис. 3.37

Рис. 3.38

Рис. 3.39

Рис. 3.40

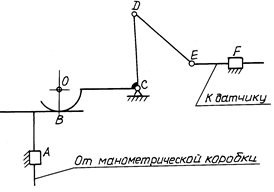
Рис. 3.41

Лекция № 4

Тема 4: Кинематический анализ плоских рычажных механизмов

4.1. Общие положения

Кинематический анализ механизмов состоит в определении движения звеньев механизма по заданному закону движения начальных звеньев.

При кинематическом исследовании механизмов рассматриваются следующие основные вопросы:

1) определение положений механизма;

2) построение траекторий точек механизма;

3) определение линейных скоростей и ускорений точек механизма;

4) определение угловых скоростей и ускорений звеньев механизма.

Эти задачи постоянно возникают в конструкторской практике. Так, исследование траекторий отдельных точек механизма позволяет вписать его в предназначенные объемы внутри общих габаритов машины. Для определения инерционных нагрузок необходимо знать ускорения. При расчете маховых масс используются скорости звеньев.

Методы кинематического анализа делятся на две группы:

1) аналитические;

2) графические, точнее, графо-аналитические.

Аналитические методы содержат достаточно сложные алгоритмы, но при использовании ПЭВМ дают высокоточные результаты при минимальных затратах времени. Графические методы достаточно наглядны и используются для составления алгоритмов, а также для анализа данных компьютерных распечаток.

Графические методы подразделяются на:

1) метод планов;

2) метод кинематических диаграмм.

4.2. Кинематические характеристики

Исходными данными для кинематического анализа являются:

– кинематическая схема механизма;

– размеры звеньев;

– угловая или линейная обобщенная координата;

– угловая или линейная скорость.

В исследуемом механизме имеется одно начальное звено или несколько звеньев, кинематика которых задана. Число таких звеньев равно числу степеней свободы механизма. Это может быть входное звено (ведущее) либо выходное. Его отличительным признаком является заданная обобщенная координата. Например, звено 1, вращающееся вокруг неподвижной оси, имеет одну степень свободы и его положение определяется одной угловой координатой j1 (рис. 4.1, а). Звено, перемещающееся поступательно относительно стойки, имеет также одну степень свободы и координату xС.

При кинематическом анализе искомыми будут угловые координаты (направляющие углы) шатуна, коромысла, кулисы и линейные координаты xS и yS ползунов и центров масс звеньев в функции времени t. Углы отсчитывают от положительного направления оси x в направлении против часовой стрелки. Начальному звену задают угловую скорость w при вращательном движении и линейную скорость  при поступательном движении.

Положительное направление угловой скорости и углового ускорения — против часовой стрелки, линейных скоростей и ускорений — по направлению оси x. Искомыми также являются линейные скорости  и ускорения a, угловые скорости w и ускорения e. Как известно, скорости определяют как первые производные от перемещения по времени:

 = ds/dt; w = dj/dt,                            (4.1)

а ускорения — как вторые производные от перемещений и первые производные от скоростей:

a = d2s/dt2 = d/dt; e = d2j/dt2 = dw/dt.               (4.2)

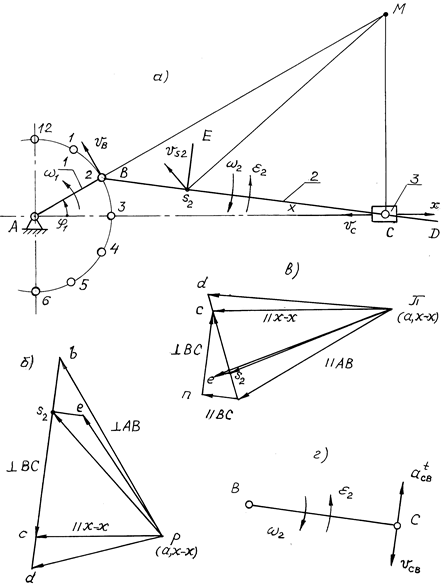
Рис. 4.1

При заданной частоте вращения n (об/мин) угловую скорость в рад/с определяют по формуле w = pn/30.

Третья производная от перемещения по времени называется градиентом ускорения (пульсом, рывком или резкостью — jerk):

j = d3s/dt3 = d2/dt2.                             (4.3)

Он характеризует изменение сил. Чем он больше, тем рассматриваемый процесс ближе к удару. Часто в аналитических методах анализа и синтеза используются аналоги скоростей и ускорений.

NB 4.1. Аналогом скорости точки называется первая производная радиуса-вектора точки по обобщенной координате.

При поступательном движении какого-либо звена и вращательном движении начального звена радиус-вектор механизма можно считать равным перемещению s. Аналог скорости

q = ds/dj = s'j = /w.                         (4.4)

Скачать файл